Table of Contents
Problem Statement
Number of Islands II LeetCode Solution – You are given an empty 2D binary grid grid of size m x n. The grid represents a map where 0‘s represent water and 1‘s represent land. Initially, all the cells grid are water cells (i.e., all the cells are 0‘s).
We may perform an add land operation which turns the water at position into a land. You are given an array positions where positions[i] = [ri, ci] is the position (ri, ci) at which we should operate the ith operation.
Return an array of integers answer where answer[i] is the number of islands after turning the cell (ri, ci) into a land.
An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are surrounded by water.
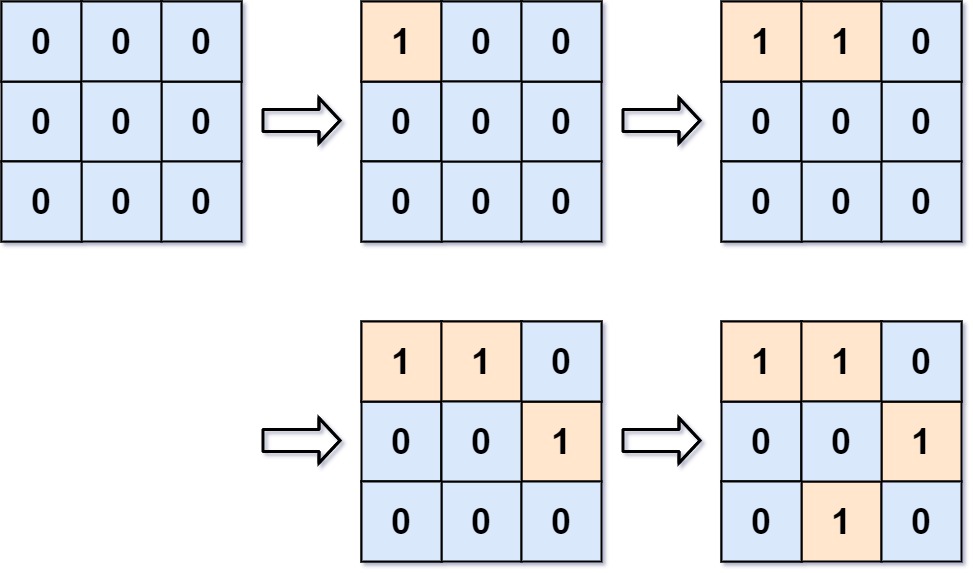
Input: m = 3, n = 3, positions = [[0,0],[0,1],[1,2],[2,1]] Output: [1,1,2,3] Explanation: Initially, the 2d grid is filled with water. - Operation #1: addLand(0, 0) turns the water at grid[0][0] into a land. We have 1 island. - Operation #2: addLand(0, 1) turns the water at grid[0][1] into a land. We still have 1 island. - Operation #3: addLand(1, 2) turns the water at grid[1][2] into a land. We have 2 islands. - Operation #4: addLand(2, 1) turns the water at grid[2][1] into a land. We have 3 islands.
Explanation
This is a basic union-find problem. Given a graph with points being added, we can at least solve:
- How many islands in total?
- Which island is point A belonging to?
- Are point tA and point B connected?
The idea is simple. To represent a list of islands, we use trees. i.e., a list of roots. This helps us find the identifier of an island faster. If roots[c] = p means the parent of node c is p, we can climb up the parent chain to find out the identifier of an island, i.e., which island this point belongs to:
Do root[root[roots[c]]]... until root[c] == c;
To transform the two-dimension problem into the classic UF, perform a linear mapping:
int id = n * x + y;
Initially assume every cell is in a non-island set {-1}. When point A is added, we create a new root, i.e., a new island. Then, check if any of its 4 neighbors belong to the same island. If not, union the neighbor by setting the root to be the same. Remember to skip non-island cells.
The UNION operation is only changing the root parent so the running time is O(1).
FIND operation is proportional to the depth of the tree. If N is the number of points added, the average running time is O(logN), and a sequence of 4N operations take O(NlogN). If there is no balancing, the worse case could be O(N^2).
Remember that one island could have a different roots[node] value for each node. Because roots[node] is the parent of the node, not the highest root of the island. To find the actual root, we have to climb up the tree by calling the findIsland function.
Code
C++ Code for Number of Islands II
class Solution {
public:
struct pair_hash {
template <class T1, class T2>
std::size_t operator () (const std::pair<T1,T2> &p) const {
auto h1 = std::hash<T1>{}(p.first);
auto h2 = std::hash<T2>{}(p.second);
return h1 ^ h2;
}
};
typedef pair<int,int> _pos;
typedef unordered_map< pair<int,int>, pair<int,int>, pair_hash> _parent_map;
typedef unordered_map< pair<int,int>, int, pair_hash> _size_map;
typedef vector<vector<char>> _grid;
int set_cnts = 0;
vector<int> numIslands2(int m, int n, vector<vector<int>>& positions) {
int rows = m, cols = n;
_grid grid(rows, vector<char>(cols,'0'));
_parent_map ps;
_size_map sz;
vector<int> result;
for(auto& pos :positions) {
int row = pos[0];
int col = pos[1];
if(grid[row][col]=='1') {
result.push_back(set_cnts);
continue;
}
grid[row][col]='1';
ps[{row, col}] = {row, col};
sz[{row, col}] = 1;
set_cnts+=1;
if(row+1 < rows && grid[row+1][col] == '1') {
UF_union(sz, ps, {row,col}, {row+1,col});
}
if(col+1 < cols && grid[row][col+1] == '1') {
UF_union(sz, ps, {row,col}, {row,col+1});
}
if(col-1 >=0 && grid[row][col-1] == '1') {
UF_union(sz, ps, {row,col}, {row,col-1});
}
if(row-1 >= 0 && grid[row-1][col] == '1') {
UF_union(sz, ps, {row,col}, {row-1,col});
}
result.push_back(set_cnts);
}
return result;
}
_pos UF_find_root(_parent_map& ps, _pos node ) {
_pos root = node;
while(ps[root] != root) {
root = ps[root];
}
return root;
}
bool UF_is_connected(_parent_map& ps, _pos node1, _pos node2) {
return UF_find_root(ps, node1) == UF_find_root(ps, node2);
}
void UF_union(_size_map& sz, _parent_map& ps, _pos node1, _pos node2) {
_pos root1 = UF_find_root(ps, node1);
_pos root2 = UF_find_root(ps, node2);
if(root1 == root2) return;
if(sz[root1] <sz[root2]) {
ps[root1] = root2;
sz[root2] += sz[root1];
} else {
ps[root2] = root1;
sz[root1] += sz[root2];
}
set_cnts--;
}
};
Java Code for Number of Islands II
class Solution {
public List<Integer> numIslands2(int m, int n, int[][] positions) {
List<Integer> result = new ArrayList<>();
if (positions == null || positions.length == 0) {
return result;
}
int[] root = new int[m * n];
Arrays.fill(root, -1);
int count = 0;
int[] xDelta = {1, -1, 0, 0};
int[] yDelta = {0, 0, 1, -1};
for (int[] position : positions) {
int x = position[0];
int y = position[1];
int index = x * n + y;
if (root[index] != -1) { // duplicate position
result.add(count);
continue;
}
count++;
root[index] = index;
for (int i = 0; i < 4; i++) {
int r = x + xDelta[i];
int c = y + yDelta[i];
if (isValid(m, n, r, c, root)) {
int neighborIndex = r * n + c;
int neighborRoot = findRoot(root, neighborIndex);
if (neighborRoot != index) {
root[neighborRoot] = index;
count--;
}
}
}
result.add(count);
}
return result;
}
private boolean isValid(int m, int n, int r, int c, int[] root) {
if (r < 0 || c < 0 || r >= m || c >= n || root[r * n + c] == -1) {
return false;
}
return true;
}
private int findRoot(int[] root, int index) {
while (index != root[index]) {
root[index] = root[root[index]];
index = root[index];
}
return index;
}
}Python Code for Number of Islands II
class UF:
def __init__(self, n):
self.parent = {i: i for i in range(n)}
self.size = {i: 1 for i in range(n)}
def find(self, x):
if x != self.parent[x]:
self.parent[x] = self.find(self.parent[x])
return self.parent[x]
def union(self, x, y):
rootX = self.find(x)
rootY = self.find(y)
if rootX == rootY:
return
if rootX <= rootY:
self.parent[rootX] = rootY
self.size[rootY] += self.size[rootX]
else:
self.parent[rootY] = rootX
self.size[rootX] += self.size[rootY]
class Solution:
def numIslands2(self, m: int, n: int, positions: List[List[int]]) -> List[int]:
uf = UF(m * n)
res = []
count = 0
visited = set()
for x, y in positions:
if (x, y) in visited:
res.append(count)
continue
count += 1
visited.add((x, y))
for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
xx, yy = x + dx, y + dy
if xx < 0 or xx == m or yy < 0 or yy == n:
continue
# skip water
if (xx, yy) not in visited:
continue
component1 = uf.find(x * n + y)
component2 = uf.find(xx * n + yy)
if component1 != component2:
uf.union(component1, component2)
count -= 1
res.append(count)
return resComplexity Analysis for Number of Islands II LeetCode Solution
Time Complexity
Space Complexity
O(mn)