The problem Partition Array Into Three Parts With Equal Sum Leetcode Solution provides us with an array or vector and asks if there are three partitions possible of the sequence. Here, by partition we mean that is there two indices i, j such that the sum of elements from start to ith index is equal to the sum of elements from i+1 to jth index. And the sum of elements from j+1 index to the last element is also equal to the first two segments of the array. If there exist such two indices, we say the array can be partitioned into three parts with an equal sum, else no. Before moving into the solution let’s see a few examples.
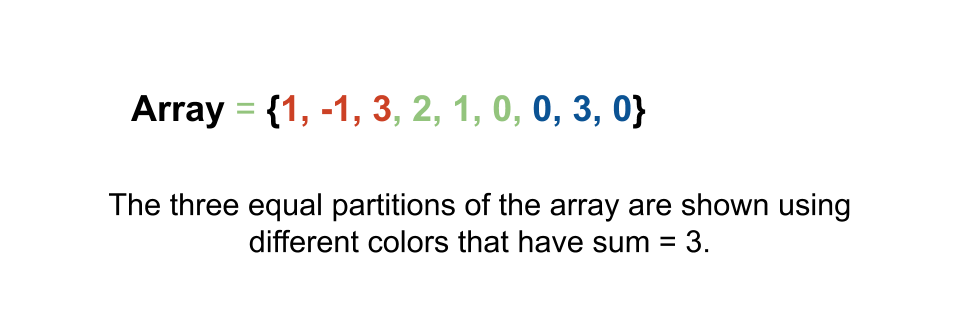
arr = [0,2,1,-6,6,-7,9,1,2,0,1]
true
Explanation: Since we can divide the array into three segments of the equal sum. Thus we can say that the array can be partitioned into three equal sums. More formally, 0 + 2 + 1 = -6 + 6 – 7 + 9 + 1 = 2 + 0 + 1.
arr = [0,2,1,-6,6,7,9,-1,2,0,1]
false
Explanation: Since there is no way to divide the array into three separate sections that have the same sums. Thus the answer is false.
Table of Contents
Approach for Partition Array Into Three Parts With Equal Sum Leetcode Solution
The problem Partition Array Into Three Parts With Equal Sum Leetcode Solution asked us if we can partition the given array into three disjoint subarrays that have equal sums. So, to solve the problem first we need to find the total sum of the array. If the total sum is not divisible by 3, then the answer is false. Because then there is no way to divide the array into three equal sub-parts. But if the sum is divisible by 3. We will check if we can attain sum/3. We simulate this process by storing the continuous sum of the elements until we find their total equal to the sum/3. If we get the total until the current element = sum/3, we reset the total to 0. And once again, start finding the total of elements = sum/3. If we can get the sum/3 3 times by this method. We can assure that we can partition the array into 3 parts else no.
Code
C++ code for Partition Array Into Three Parts With Equal Sum Leetcode Solution
#include <bits/stdc++.h>
using namespace std;
bool canThreePartsEqualSum(vector<int>& arr) {
int sum = 0;
for(int i=0;i<arr.size();i++)
sum += arr[i];
if(sum % 3 != 0)
return false;
int sum3 = sum/3, partitions = 0;
sum = 0;
for(int i=0;i<arr.size();i++){
sum += arr[i];
if(sum == sum3){
++partitions;
sum = 0;
}
}
return partitions >= 3;
}
int main() {
vector<int> arr({0,2,1,-6,6,-7,9,1,2,0,1});
cout<<canThreePartsEqualSum(arr);
return 0;
}true
Java code for Partition Array Into Three Parts With Equal Sum Leetcode Solution
import java.util.*;
import java.lang.*;
import java.io.*;
class Main
{
public static boolean canThreePartsEqualSum(int[] arr) {
int sum = 0;
for(int i=0;i<arr.length;i++)
sum += arr[i];
if(sum % 3 != 0)
return false;
int sum3 = sum/3, partitions = 0;
sum = 0;
for(int i=0;i<arr.length;i++){
sum += arr[i];
if(sum == sum3){
++partitions;
sum = 0;
}
}
return partitions >= 3;
}
public static void main (String[] args) throws java.lang.Exception{
int[] arr = {0,2,1,-6,6,-7,9,1,2,0,1};
System.out.print(canThreePartsEqualSum(arr));
}
}true
Complexity Analysis
Time Complexity
O(N), even though we have traversed the array twice. But this will count as linear time complexity because the times we traverse the array does not depend on its size.
Space Complexity
O(1), since we used a constant number of elements and did not store some specific information regarding each index. The space complexity is constant.