Path Crossing Leetcode Solution

Problem Statement

In path crossing problem a_string is given in which there are only four different characters ‘N’, ‘S’, ‘E’ or ‘W’ showing the movement of an object in one direction at a time by 1 unit. Object is initially at origin (0,0). We have to find out if the object will cross its path at any point walking along the path specified in the given string.

Example

path = "NES"

false

Explanation:

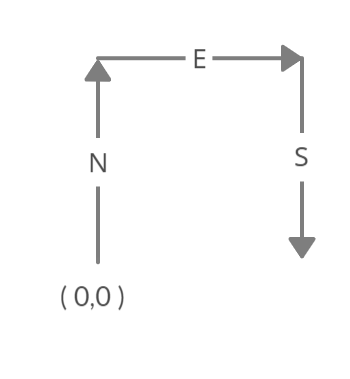
Notice that the path doesn’t cross any point more than once.

path = "NESWW"

true

Explanation:

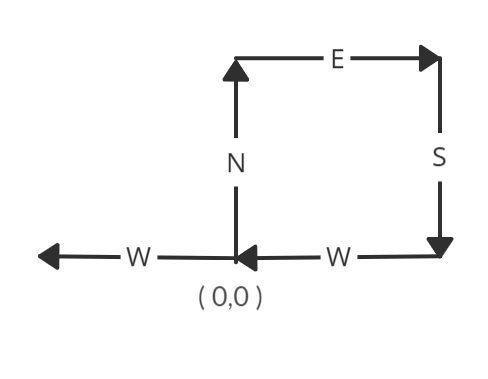
Notice that the path visits the origin twice.

Approach

From the problem statement it is clear that if a coordinate (x,y) occurs in the path of the object, then it must be the position of the object after certain number of moves as it is moving with 1 unit each time.
So if a point comes in its path which is once previously visited, then it is surely crossing the path. So we can return true as soon as we found this kind of point.

Now how do we know that a point has been visited previously. For this we can use a Hash Set and keep storing all the points in its path. At any time if we found that the next point to which object is going is already present in the set, we return true. After completing the path if this doesn’t happens, then we return false.

Algorithm :

1. Create a hash set of keys, where key represents coordinate (x,y). For this we can use pair<int,int> as key Or we can use a simple string that should represent two integers uniquely. Ex- “2_3” for representing coordinate (2,3).
2. Create two variable x and y. Initialise them with the origin coordinate (0,0) and insert it in the set.
3. Run a loop for iterating the specified moves. Increment or decrement the value of x or y according to current move as follows:
   ‘N’ means new coordinate is (x,y+1)
   ‘E’ means new coordinate is (x+1,y)
   ‘S’ means new coordinate is (x,y-1)
   ‘W’ means new coordinate is (x-1,y)
4. Check whether the coordinate (x,y) is present in the set or not. If present then return true, Else add this coordinate into the set and continue.
5. After completion of loop if no crossing is found the return false.

Implementation

C++ Program for Path Crossing Leetcode Solution

#include <bits/stdc++.h>
using namespace std;

bool isPathCrossing(string path) 
{
    set< pair<int,int> > s;
    int x=0,y=0;
    s.insert({x,y});

    for(char c: path)
    {
        if(c=='N') y++;
        if(c=='E') x++;
        if(c=='S')  y--;
        if(c=='W')  x--;

        if(s.count({x,y}))
        return true;

        s.insert({x,y});
    }

    return false;
}

int main() 
{
    string path = "NESWW";
    if(isPathCrossing(path))
        cout<<"true"<<endl;
    else
        cout<<"false"<<endl;

  return 0; 
}

true

Java Program for Path Crossing Leetcode Solution

import java.lang.*;
import java.util.*;

class PathCrossing
{  
    public static boolean isPathCrossing(String path) 
    {
        Set<String> set=new HashSet<String>();

        int x=0,y=0;
        String key= x + "_" + y;

        set.add(key);

        for(int i=0;i<path.length();i++)
        {
            char c= path.charAt(i);
            if(c=='N') y++;
            if(c=='E') x++;
            if(c=='S') y--;
            if(c=='W') x--;

            key= x + "_" + y;
            if(set.contains(key)) return true;

            set.add(key);
        }

        return false;
    }
    
    public static void main(String args[])
    {
       String path = "NESWW";
  
       System.out.println(isPathCrossing(path));
        
    }
}

true

Complexity Analysis for Path Crossing Leetcode Solution

Time Complexity

O(N) : where N is the size of the given string. As we visit each character in the string only once, therefore time complexity is O(N).

Space Complexity 

O(N) : Extra memory we are using to store the visited coordinates in a set.