Sliding Window Median Leetcode Solution

Problem Statement

The Sliding Window Median LeetCode Solution – “Sliding Window Median” states that given an integer array nums and an integer k, where k is the sliding window size. We need to return the median array of each window of size k.

Example:

Input:  [1,3,-1,-3,5,3,6,7], k = 3

Output: [1.00000,-1.00000,-1.00000,3.00000,5.00000,6.00000]

Explanation:

• Median of [1, 3, -1], [3, -1, -3], [-1, -3, 5], [-3, 5, 3], [5, 3, 6], [3, 6, 7] are [1, -1, -1, 3, 5, 6].

Input:  nums = [1,2,3,4,2,3,1,4,2], k = 3

Output: [2.00000,3.00000,3.00000,3.00000,2.00000,3.00000,2.00000]

Explanation:

• The median of all sliding windows of size k is: [2, 3, 3, 3, 2, 3, 2].

Approach

Idea:

1. The main idea to solve this problem is to use Hashset or PriorityQueue.
2. The idea is similar to the problem Median of Stream of Integers. Here, we need to find the median of every subarray of size k efficiently.
3. Maintain two hash sets (multiset in C++), called as left and right which will store k integers of a subarray of size k, ending at position i.
4. The left set will store first (k+1)/2  smallest integers of the subarray while the right set will store k/2 greatest integers of the subarray at any step.
5. Remember that size of the left set will be either equal to the size of the right set or, greater than the size of the right set by exactly 1.
6. Iterate for the first k elements of the array and store these integers in the left and right sets such that the above criteria holds for both sets.
7. Note that, we will balance the sets if the size of the left set minus the size of the right set is strictly greater than 1 or if the size of the right set is strictly greater than 1.
8. Now, when k is odd median is the topmost element of the left set.
9. When k is even, the median is the average of the topmost elements of both sets.
10. We’ll iterate for the remaining elements and delete the element present at (i-k)th position from the sets and insert the element present at the current position and balance the sizes of the two sets and find the median corresponding to the current state of the sets.
11. Finally, return the answer array.
12. Check the sample illustration.

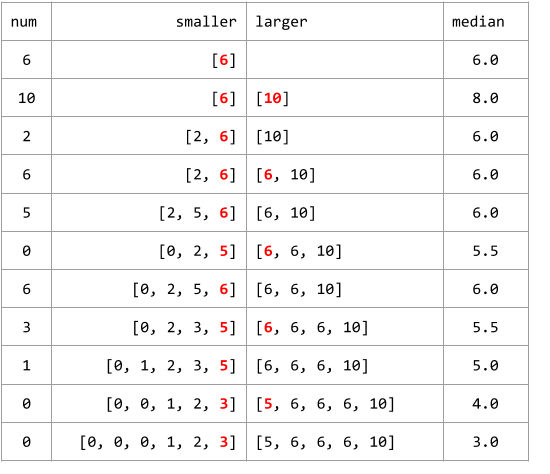
Code

Sliding Window Median Leetcode C++ Solution:

class Solution {
public:    
    #define ll long long
    
    multiset<ll> right;
    multiset<ll,greater<ll>> left;
    
    double GetMedian(){
        int n = left.size() + right.size();
        if(n&1){
            return (double)*left.begin();
        }
        return ((double)(*left.begin()+*right.begin()))/2.0;
    }
    
    void BalanceSets(){
        while((int)right.size()>(int)left.size()){
            left.insert(*right.begin());
            right.erase(right.begin());
        }
        while((int)left.size()-(int)right.size()>1){
            right.insert(*left.begin());
            left.erase(left.begin());
        }
    }
    
    vector<double> medianSlidingWindow(vector<int>& nums, int k) {
        int n = nums.size();
        for(int i=0;i<k;i++){
            if(left.empty()){
                left.insert(nums[i]);
            }
            else if(right.empty()){
                if(nums[i]<*left.begin()){
                    right.insert(*left.begin());
                    left.erase(left.begin());
                    
                    left.insert(nums[i]);
                }
                else{
                    right.insert(nums[i]);
                }
            }
            else{
                if(nums[i]<=*left.begin()){
                    left.insert(nums[i]);
                }
                else{
                    right.insert(nums[i]);
                }
            }
            
            BalanceSets();            
        }
        
        vector<double> ans = {GetMedian()};
        
        for(int i=k;i<n;i++){
            if(nums[i]<=*left.begin()){
                left.insert(nums[i]);
            }
            else{
                right.insert(nums[i]);
            }
            if(left.count(nums[i-k])){
                left.erase(left.find(nums[i-k]));
            }
            else{
                right.erase(right.find(nums[i-k]));
            }
            BalanceSets();
            
            ans.push_back(GetMedian());            
        }
        return ans;
    }
};

Sliding Window Median Leetcode Java Solution:

class Solution {
    public double[] medianSlidingWindow(int[] nums, int k) {
        Comparator<Integer> comparator = (a, b) -> nums[a] != nums[b] ? Integer.compare(nums[a], nums[b]) : a - b;
        TreeSet<Integer> left = new TreeSet<>(comparator.reversed());
        TreeSet<Integer> right = new TreeSet<>(comparator);

        Supplier<Double> median = (k % 2 == 0) ?
            () -> ((double) nums[left.first()] + nums[right.first()]) / 2 :
            () -> (double) nums[right.first()];

        Runnable balance = () -> { while (left.size() > right.size()) right.add(left.pollFirst()); };

        double[] result = new double[nums.length - k + 1];

        for (int i = 0; i < k; i++) left.add(i);
        balance.run(); result[0] = median.get();

        for (int i = k, r = 1; i < nums.length; i++, r++) {
            if(!left.remove(i - k)) right.remove(i - k);

            right.add(i); left.add(right.pollFirst());

            balance.run(); result[r] = median.get();
        }

        return result;
    }
}

Complexity Analysis for Sliding Window Leetcode Solution

Time Complexity

The time complexity of the above code is O(Nlog(K)) since we traverse the entire input array once and for each position, we’re working with set/heap insertion and deletion which takes log(K). Here, N is the size of the input array and k is the length of the sliding window.

Space Complexity

The space complexity of the above code is O(K) since we’re maintaining a heap/set of maximum size K.