Split a String in Balanced Strings Leetcode Solution

Problem Statement

In this problem, we are given a string of characters, containing only ‘R’ and ‘L’. We call a string balanced if it has the same number of ‘R’s and ‘L’s. We can split the given string into disjoint substrings. The goal is to find the maximum possible number of balanced split strings.

Note:

• The given string is balanced.
• Length of the string lies in the range: [1, 1000]
• Only ‘L’ and ‘R’ are present in the input

Example

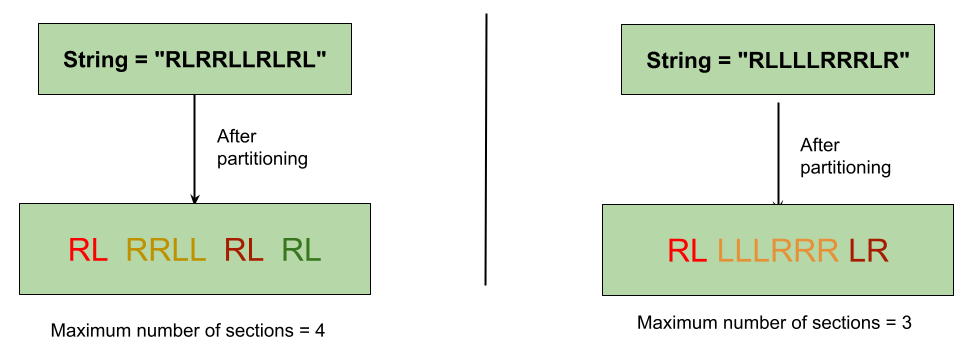
s = "RLRRLLRLRL"

4

s = "RLLLLRRRLR"

3

Explanation:

Approach (Greedy)

Therefore, we will at least have 1 possible balanced split. Now, we need to maximize this number of splits to get max number of partitions. Intuitively, we can solve it greedily. We will traverse the string, and at every point where we have received an equal number of ‘L’s and ‘R’s, we will increment the number of possible sections. This way, we will consider every solution for a balanced split string.

Implementation of Split a String in Balanced Strings Leetcode Solution

C++ Program

#include <bits/stdc++.h>

using namespace std;

int balancedStringSplit(string s) {
    int balance = 0 , splits = 0;
    for(char &c : s) {
        balance += (c == 'L' ? -1 : 1);
        if(balance == 0)
            splits++;
    }
    return splits;
}

int main() {
    string s = "RLRRLLRLRL";
    cout << balancedStringSplit(s) << endl;
    return 0;
}

Java Program

import java.util.*;
import java.io.*;

class balanced_splits {
    public static int balancedStringSplit(String s) {
        int balance = 0 , splits = 0;
        for(int i = 0 ; i < s.length() ; i++) {
            char c = s.charAt(i);
            balance += (c == 'L' ? -1 : 1);
            if(balance == 0)
                splits++;
        }
        return splits;
    }

    public static void main(String args[]) {
        String s = "RLRRLLRLRL";
        System.out.println(balancedStringSplit(s));
    }
}

4

Complexity Analysis of Split a String in Balanced Strings Leetcode Solution

Time Complexity

O(N), N = length of the string. The time complexity is linear because we traverse the whole string once.

Space Complexity 

O(1), as we only use constant memory space.