In Subset Leetcode problem we have given a set of distinct integers, nums, print all subsets (the power set).
Note: The solution set must not contain duplicate subsets.
An array A is a subset of an array B if a can be obtained from B by deleting some (possibly, zero or all) elements.
Table of Contents
Example
Input:
[1, 2, 3]
Output:
[1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]
Approach 1: Iterative solution using bit manipulation
Each subset of a set of n elements can be represented as a sequence of n bits, which corresponds to an integer between 0…2n-1. The ones in the bit sequence indicate which elements are included in the subset.
Algorithm
- Declare an array of vectors “ans” in which we will store our all subsets.
- Initialize a variable n which represents the size of the nums_array.
- Run a loop for I in range 0 to 2n-1
- Initialize an array “temp” in which we will store our current subset.
- Run a loop for j in range 0 to n-1
- If the jth bit of I is set, then add the nums[i] to the temp array.
- Add the “temp” array to “ans”
- Print the final ans array.
Implementation for Print All Subsets
#include <bits/stdc++.h>
using namespace std;
int main()
{
vector<int> nums = {1, 2, 3};
vector<vector<int>> ans;
for (int i = 0; i < (1 << (nums.size())); i++)
{
vector<int> temp;
for (int j = 0; j < nums.size(); j++)
{
if (i & (1 << j))
{
temp.push_back(nums[j]);
}
}
ans.push_back(temp);
}
for (auto x : ans)
{
if(x.size()>0)
cout<<"[";
for (auto y : x)
{
if(y==x[x.size()-1])
cout << y <<"]";
else
cout << y <<", ";
}
cout << endl;
}
return 0;
}
[1] [2] [1, 2] [3] [1, 3] [2, 3] [1, 2, 3]
Complexity Analysis for Print All Subsets
Time complexity
We run two nested loops, one of range 2^n and the other of range n. so the final time complexity is O(2^n*n).
Space complexity
There are 2^n-1 subsets and for every subset, we need O(n) space on average so total space complexity is O(2^n * n).
Can we optimize it?
Yes, we can optimize it using backtracking, let’s see how!
Approach 2: Recursive solution using backtracking
We iterate over the nums array and for each position we have two choices, either take the ith element or skip it.
Algorithm
- Create a function that takes the arguments, final answer array, current subset array, input array, and a variable “index” which points to the current element in the nums array.
- Base condition: If the “index” is equal to the size of the nums array then add our current subset array to the final answer because now we cannot traverse the nums array anymore.
- We have two choices now
- Skip the current element and call the recursive function with index+1 and all other arguments will remain the same.
- Add the current element to the current subset and call the recursive function with index +1 and other arguments. After calling the recursive function, do the backtracking step by removing the last element from the current subset.
- Print the final answer.
Understand with example
Let’s take an input array nums = [1,2,3]
Then the recursion tree will look like this:
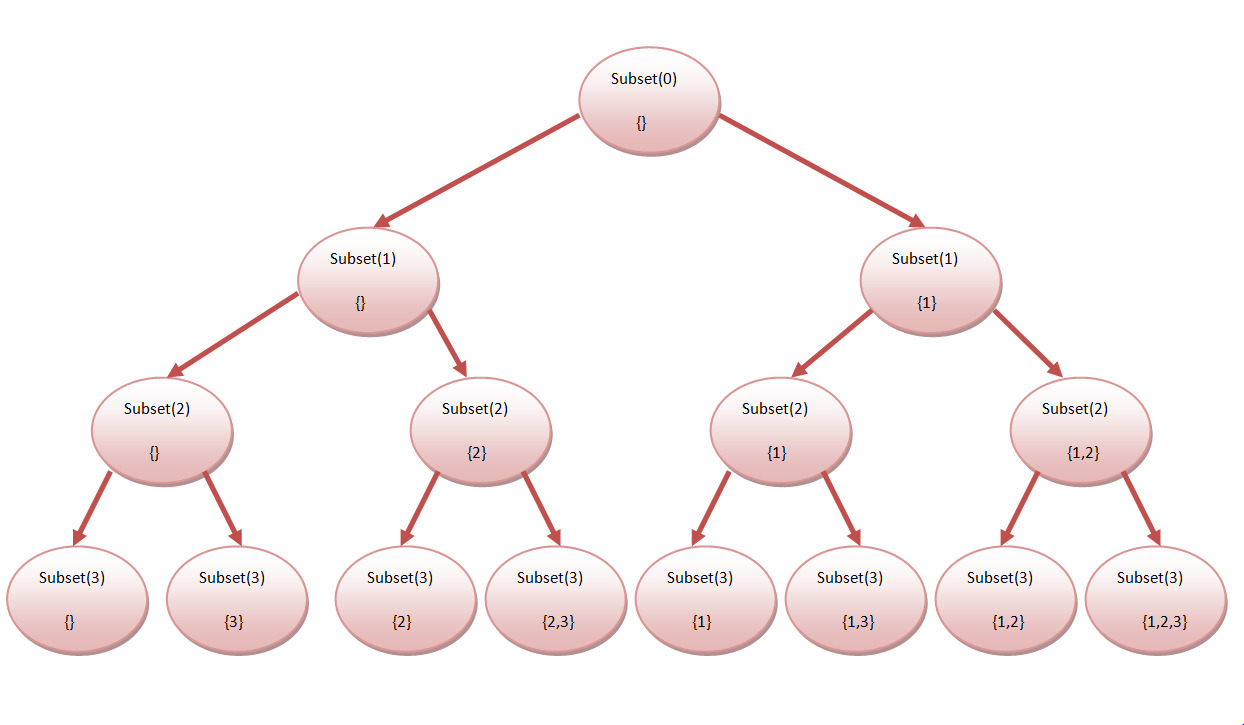
In the above tree, Subset(i) is the recursive function where i denotes the current index.
Implementation for Print All Subsets
C++ program for Subset Leetcode
#include <bits/stdc++.h>
using namespace std;
void subsets(vector<vector<int>> &ans, vector<int> &temp, vector<int> &nums, int i)
{
if (i == nums.size())
{
ans.push_back(temp);
return;
}
subsets(ans, temp, nums, i + 1);
temp.push_back(nums[i]);
subsets(ans, temp, nums, i + 1);
temp.pop_back();
return;
}
int main()
{
vector<int> nums = {1, 2, 3};
vector<vector<int>> ans;
vector<int> temp;
subsets(ans, temp, nums, 0);
for (auto x : ans)
{
if(x.size()>0)
cout<<"[";
for (auto y : x)
{
if(y==x[x.size()-1])
cout << y <<"]";
else
cout << y <<", ";
}
cout << endl;
}
return 0;
}
[3] [2] [2, 3] [1] [1, 3] [1, 2] [1, 2, 3]
JAVA program for Subset Leetcode
import java.util.*;
public class Main
{
static List<List<Integer>> res;
public static void subsets(int[] nums,int index,List<Integer> list){
if(index==nums.length-1){
res.add(new ArrayList<Integer>(list));
list.add(nums[index]);
res.add(new ArrayList<Integer>(list));
list.remove(list.size()-1);
return;
}
subsets(nums,index+1,list);
list.add(nums[index]);
subsets(nums,index+1,list);
list.remove(list.size()-1);
}
public static void main(String[] args) {
res = new ArrayList<>();
int[] nums={2, 3, 4};
List<Integer> list = new ArrayList<Integer>();
subsets(nums, 0, list);
for(List<Integer> subset:res){
for(int i: subset){
System.out.print(i+", ");
}
System.out.println();
}
}
}
4, 3, 3, 4, 2, 2, 4, 2, 3, 2, 3, 4,
Complexity Analysis for Subset Leetcode
Time complexity
For every index, we make 2 recursion calls and there are n elements so total time complexity is O(2^n).
Space complexity
There are 2^n-1 subsets and for every subset, we need O(n) space on average so total space complexity is O(2^n * n).