Symmetric Tree Leetcode Solution

Difficulty Level Easy
Frequently asked in Adobe Amazon Apple Bloomberg Facebook Google LinkedIn Microsoft Oracle Uber
Binary Tree Breadth First Search Depth First Search TreeViews 3951

Problem Statement

The Symmetric Tree LeetCode Solution – “Symmetric Tree” states that given the root of the binary tree and we need to check if the given binary tree is a mirror of itself (symmetric around its center) or not? If Yes, we need to return true otherwise, false.

Example:

Symmetric Tree Leetcode Solution

 

Note that nodes with the same color have the same node value. The binary tree is a Symmetric Tree.

Input:  root = [1,2,2,3,4,4,3]
Output: true

Explanation:

  • Check the above diagram for a better understanding.
Input:  root = [1,2,2,null,3,null,3]
Output: false

Symmetric Tree Leetcode Solution

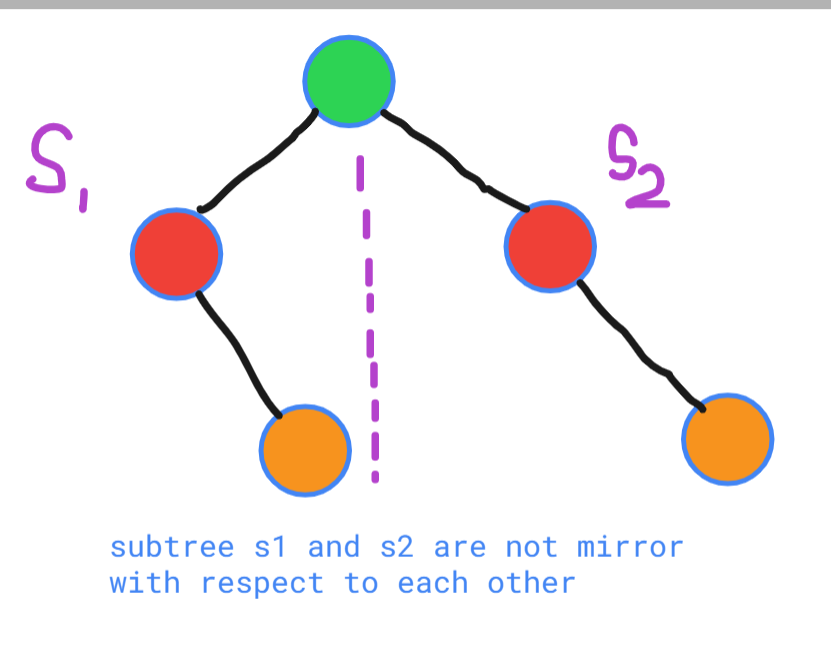
Explanation:

  • Check the above diagram for a better understanding.

Approach

Idea:

  1. The main idea to solve this problem is to use Recursion.
  2. Now, a tree is called symmetric if the left subtree must be a mirror reflection of the right subtree.
  3. Also, Two trees are said to be a mirror with respect to each other if:
    1. Their roots are of the same value.
    2. The right subtree of each tree is a mirror reflection of the left subtree of another tree.
  4. So, perform the recursion with the following cases:
    1. For the base case:
      • If both root nodes are null pointers, return true.
      • If exactly one of them is a null node, return false.
    2. In general:
      • Root nodes must have the same value and,
      • The left subtree and right subtree must be the mirror reflection with respect to each other.
      • So, return true if the root node’s values are the same and left as well as right subtrees are symmetric.

Code

Symmetric Tree Leetcode C++ Solution:

class Solution {
public:
    bool check(TreeNode* root1,TreeNode* root2){
        if(root1==nullptr or root2==nullptr){
            return root1==root2;
        }
        return root1->val==root2->val and check(root1->left,root2->right) and check(root1->right,root2->left);
    }
    bool isSymmetric(TreeNode* root) {
        return check(root,root);
    }
};

Symmetric Tree Leetcode Java Solution:

class Solution {
    private boolean check(TreeNode root1,TreeNode root2){
        if(root1==null || root2==null){
            return root1==root2;
        }
        return root1.val==root2.val && check(root1.left,root2.right) && check(root1.right,root2.left);
    }
    public boolean isSymmetric(TreeNode root) {
        return check(root,root);
    }
}

Complexity Analysis for Symmetric Tree Leetcode Solution

Time Complexity

The time complexity of the above code is O(N) since we traverse the entire input tree once where N = the total number of nodes in the tree.

Space Complexity

The space complexity of the above code is O(N) [considering recursive calls also]. The number of recursive calls is bounded by the height of the tree and in the worst case, the tree can be linear. Hence, Space Complexity is O(N).

Translate »