XOR Operation in an Array Leetcode Solution TutorialCup

Table of Contents

Problem Statement

In this problem we have to do XOR Operation in an Array of size n in which each element is equal to (start + 2*i) where i is the index of the element (0-indexed) and value of start is given.
We have to return the bitwise XOR of all elements of the array.

Example

n = 4, start = 3

Explanation:

Array nums is equal to [3, 5, 7, 9] where (3 ^ 5 ^ 7 ^ 9) = 8.
Where “^” corresponds to bitwise XOR operator.

n = 1, start = 7

Explanation:

Array nums is equal to [7] , Hence xor = 7.

Approach (Brute Force)

We can simply run a for loop n times for i=0 to i=n-1. In for loop we will be doing bitwise xor of (start+2*i) with the current xor which we will store in a variable res.

Algorithm

1. create a variable ind to represent index of the element of the array and initialize with 0.
2. create a variable res to store the current xor during for loop and initialize with 0.
3. Run a for loop from ind=0 to ind=n-1.
4. Do bitwise xor of res with (start+ 2*i) i.e. element at index ind and store the result in res.
5. Return the res.

Implementation for XOR Operation in an Array Leetcode Solution

C++ Program

#include <bits/stdc++.h>
using namespace std;

int xorOperation(int n, int start) {

    int ind=0;
    int res=0;
    for(ind=0;ind<n;ind++) res=res^(start+2*ind);

    return res;

}
int main() 
{
        int n=4;
        int start=3;
    cout<<xorOperation(n,start)<<endl;

  return 0; 
}

Java Program

import java.lang.*;

class XorOperation
{  
    public static int xorOperation(int n, int start) 
    {

        int ind=0;
        int res=0;
        for(ind=0;ind<n;ind++) res=res^(start+2*ind);

        return res;      
    }
    
    
    public static void main(String args[])
    {
        int n=4;
        int start=3;

        System.out.println(xorOperation(n,start));
        
    }
}

Complexity Analysis for XOR Operation in an Array Leetcode Solution

Time Complexity

O(N): Where N is the given size of the array. As we are traversing the array in a single for loop for N elements. Hence time complexity is O(N).

Space Complexity

O(1): As we are not using any extra memory other than some variables. Hence extra space utilized is constant.

Approach (Bit Manipulation)

In the above problem we can see that difference between each next element is 2. That means either all the elements will be even or all will be odd. That makes a kind of a range but not consecutive i.e. it is having alternate values.

Using bit manipulation we can find bitwise xor of a range having consecutive elements in it in constant time. Let us see how, and then we will try to convert above problem into the problem below:

Lets suppose a range =[3,4,5,6,7,8,9,10] , and we have to apply xor in the range between first and last element.

Let x be any even number and y be the number next to x. i.e. y=x+1. We can easily analyze that xor of x and y will always be 1. Or xor of every even number and odd number next to it is always 1. Hence we can conclude that every even-odd pairs between first and last number gives xor equal to 1.
i.e. 4^5=1, 6^7=1, 8^9=1

Now if the number of those pairs are odd then xor of the elements between 1st even number and last odd number will be 1, or else 0.
i.e. 4^5^6^7^8^9 = 1^1^1 = 1

Now we are only left with the numbers at the end positions which is 3 and 10. Hence our answer will be 3^1^10 = 8 as shown in figure below:

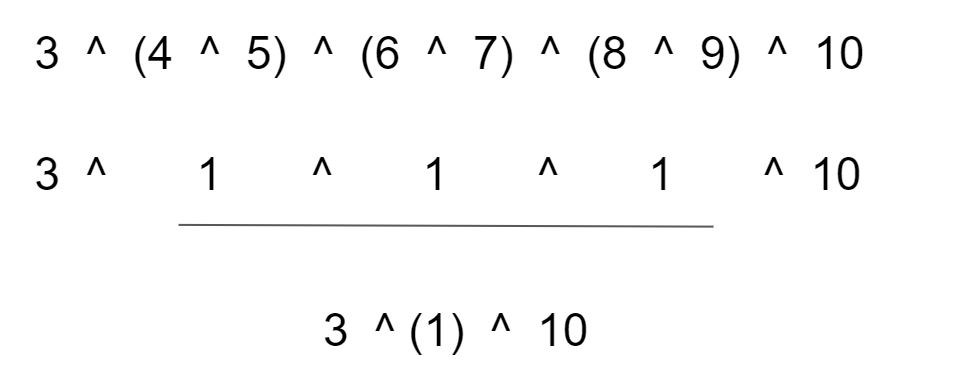
XOR Operation in an Array Leetcode Solution

Converting the problem into consecutive range XOR

In the above problem we can reduce the distance between each element from 2 to 1 if we right shift bitwise each element by 1 ( same as dividing by 2 ). By doing this we are only affecting the last bit of the elements. So we first store the last bit of our ans by following cases :

1. If all the elements in array is odd and total number of elements is also odd, then lastbit=1.
2. Else lastbit=0.

Now after we right shift each element by 1, our range becomes :

start/2, start/2 +1 , start/2 +2 , . . . . , start/2 +(n-1) .

Where first= start/2 and last= start/2 + (n-1).

Now we can easily find out the xor of this range by finding bitwise xor of end elements and all even-odd pairs between them in constant time.

After finding xor we have to bitwise left shift the result by 1 to gain the original position of bits in our final answer. Finally add the lastbit to the result and return it.