Table of Contents
Problem Statement
The problem “Newman-Conway Sequence” states that you are given an input integer “n”. Then you need to print first nth element of the Newman-Conway Sequence.
Example
n = 6
4
n = 10
6
Explanation
Since the output elements represent the sixth and tenth element of the Newman-Conway Sequence. The output is absolutely correct.
Approach to find Newman-Conway Sequence
The Newman-Conway Sequence is a sequence whose each term satisfies the following recurrence relation.
P(1) = P(2) = 1
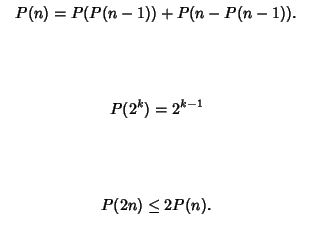
Now we need to print the nth number from the sequence. There can be two methods because each element of the sequence is dependent on the previously generated elements. So, one of the ways is to use recursion but this method is inefficient. Because we will be solving for each element many times, as we keep on calculating for higher terms in the series. Thus we need to perform a much more number of computations. So to resolve this problem of re-computation. We may use Dynamic Programming which can highly improve the efficiency of the algorithm. Currently, the recursive algorithm needs exponential time complexity. We can reduce it to a linear solution because there is only a single state.
So, in the dynamic programming solution. We will create an array that will store the elements which come before the nth element. That is all the elements from the first element to (n-1)th element. Then using these precomputed we will find our nth element. Since we have all the numbers which need to precomputed before nth number. We can easily use these values instead of calculating the required elements again and again. This technique is used to reduce the time complexity of
Code
C++ code to find nth Newman-Conway Sequence element
#include <bits/stdc++.h>
using namespace std;
int main(){
// element to be printed
int n;cin>>n;
int dp[n+1];
dp[0] = 0;
dp[1] = dp[2] = 1;
for(int i=3;i<=n;i++)
dp[i] = dp[dp[i-1]] + dp[i-dp[i-1]];
cout<<dp[n];
}6
4
Java code to find nth Newman-Conway Sequence element
import java.util.*;
class Main{
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
// eleemnt to be printed
int n = sc.nextInt();
int dp[] = new int[n+1];
dp[0] = 0;
dp[1] = 1;
dp[2] = 1;
for(int i=3;i<=n;i++)
dp[i] = dp[dp[i-1]] + dp[i-dp[i-1]];
System.out.print(dp[n]);
}
}6
4
Complexity Analysis
Time Complexity
O(N), because we simply ran a single loop to find the nth element of the sequence. Thus the time complexity is linear.
Space Complexity
O(N), since we have used a DP array to store the intermediate results which were required for the computation of nth element. The space complexity is also linear.