Table of Contents
Problem Statement
In this problem we have to find out how many trailing zeroes will be there in n!
Given n as input.
Like there is one trailing zero in 5!
5! = 5*4*3*2*1 = 120
Example
n = 3
0
Explanation: 3! = 6, no trailing zero
n = 0
0
Explanation: 0! = 1, no trailing zero
To find the number of trailing zeroes in n! , a simple way is to calculate the n! and check how many zeroes are there at the end. This we can do simply by checking if dividing the number by 10 we get remainder 0 and then removing the last zero by dividing it by 10. We can count this till we get remainder equal to zero each time.
But this approach is not practical with simple integers because we know n! is a very big number. In C++ and Java simple integer size is 64-bit at best which can only store an integer to a limit of 2^63 – 1. Which is approximate to 10^18. In java we can use BigInteger class to store big numbers like n!. But this brute force approach has large time and space complexity.
Here we are going to discuss efficient solution for finding the trailing zeroes in n!
Approach 1 (Counting factors of 5)
We can say that total number of trailing zeroes will be equal to count of how many times 10 is factor of that number. And we know that every 10 is formed of the product of two prime numbers 2 and 5.
So if we find out how many factors of 2’s are there in the number. Similarly how many factors of 5’s are there. Then we can say that each of these will combine to make product equal to 10. Therefore total number of trailing zeroes will be equal to minimum( count of 2’s , count of 5’s).
Now we have to count these factors in n!.
n! = 1*2*3 …..*(n-1)*n
So we will iterate over all the numbers from 2 to n ( incrementing by 2 because they are the numbers which contain at least one 2’s ).
For each number we will repeatedly divide it by 2 till it is divisible by 2 to find the count of 2’s in factorization of that number.
Similarly to find the count of 5’s in that number we will do same thing.
Now we will return the minimum out of these two counts.
This works but we can also optimize it a little bit. We can analyse that we have numbers from 1 to n, so we would always get 2’s powers more than 5’s powers.
Like till 4 we get two numbers which have 2 as a factor(2 and 4). At 5 we get first number having 5 as factor. So this will go on and on with similar (increasing) count difference. Here’s a visualisation that illustrates how the density between 2 factors and 5 factors differs.
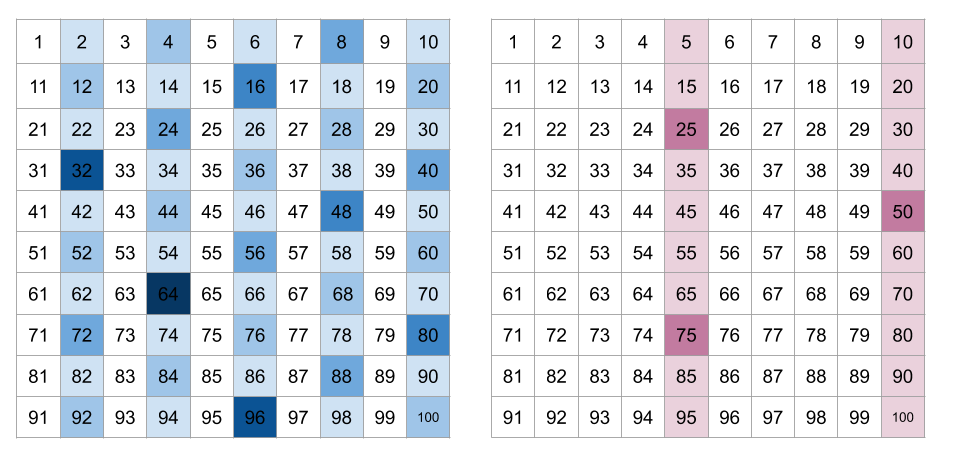
Therefore we can conclude that the count of 2 is always greater than count of 5 in n!.
So we need to find the count of 5’s only and that will be the ans. This way we reduce the task by half.
Implementation for Factorial Trailing Zeroes Leetcode Solution
C++ Program
#include <bits/stdc++.h>
using namespace std;
int trailingZeroes(int n)
{
int fives=0;
for(int i=5;i<=n;i+=5)
{
int x=i;
while(x>0 && x%5==0)
{
++fives;
x/=5;
}
}
return fives;
}
int main()
{
cout<<trailingZeroes(5)<<endl;
return 0;
}
1
Java Program
class Rextester{
public static int trailingZeroes(int n)
{
int fives=0;
for(int i=5;i<=n;i+=5)
{
int x=i;
while(x>0 && x%5==0)
{
++fives;
x/=5;
}
}
return fives;
}
public static void main(String args[])
{
System.out.println(trailingZeroes(5));
}
}
1
Complexity Analysis for Factorial Trailing Zeroes Leetcode Solution
Time Complexity
O(n) : we are iterating over all the multiples of five till n. It might look like for each element we are taking log(n) time to find the count of fives. But it amortizes to O(1) because a vast majority of numbers we checked contains only single factor of five. Hence total time complexity remains as O(n).
Space Complexity
O(1) : No any extra memory is used.
Approach 2 (Counting Factors of 5 Efficiently)
In above approach we saw that we need to find the count of 5’s only as factor of the given n!. In above approach we looped over all multiples of 5 and added count of 5’s for each number and got our ans in linear time. We will make one final observation which will allow us to calculate the ans in logarithmic time.
In n! (i.e. from 1 to n) we have some numbers which are not divisible by 5 (contributing 0 for 5’s count), then we have some numbers which are divisible by 5 (each contributing one count), then we have numbers which are divisible by 25 ( this time one extra contribution from these many numbers), then divisible by 125 ( one extra contribution from these) , like this and so on.
Then our ans will be the sum of these all contributions.
We can sum up all these as below:
total count of 5’s = n/5 + n/25 + n/125 + …. so on
This will go till denominator is less than n because after that integral value of the fraction will be zero.
Step:
Initialize denominator variable with 5.
Run a loop, in each iteration add n/denominator value to result and multiply the denominator by 5. Run the loop till denominator < n.
Implementation for Factorial Trailing Zeroes Leetcode Solution
C++ Program
#include <bits/stdc++.h>
using namespace std;
int trailingZeroes(int n)
{
int fives=0;
int den=5;
while(den <= n)
{
fives += n/den;
den *= 5;
}
return fives;
}
int main()
{
cout<<trailingZeroes(5)<<endl;
return 0;
}
1
Java Program
#include <bits/stdc++.h>
using namespace std;
int trailingZeroes(int n)
{
int fives=0;
int den=5;
while(den <= n)
{
fives += n/den;
den *= 5;
}
return fives;
}
int main()
{
cout<<trailingZeroes(5)<<endl;
return 0;
}
1
Complexity Analysis for Factorial Trailing Zeroes Leetcode Solution
Time Complexity
O(log(n)) : we are multiplying denominator by 5 each time till it is less than n. Hence total number of iteration will be log(n).
Space Complexity
O(1) : No any extra memory is used.