An array of size n has been given as an input value. The problem “Count and Toggle Queries on a Binary Array” asks to perform some of the queries which are given below, queries can vary in a random manner.
The queries are ⇒
Toggle query ⇒ toggle(starting, ending), this toggle query means, change 0s into 1 or 1s into 0s within the given range.
Count query ⇒ count(starting, ending), this count query means to count all the number of ones within the given range.
Table of Contents
Example
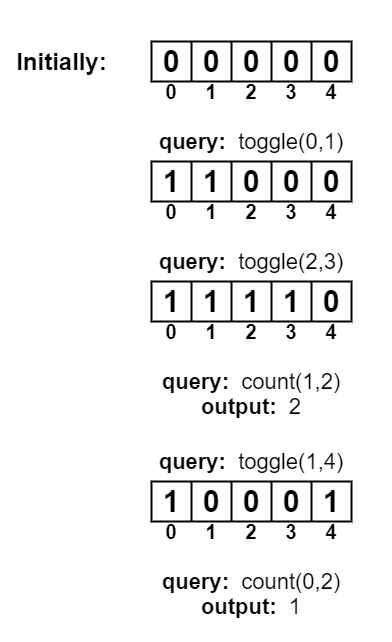
n = 5 toggle(0, 1) toggle(2, 3) count(1, 2) toggle(1, 4) count(0, 2)
Count of all the ones within the range 1 and 2 is 2. The count of all the ones within the range 0 and 2 is 1.
Explanation: The count of one is printed on each count query.
Algorithm
- Check if the Boolean boolTree is true or false. If it is true then mark that node as false. Update the value in segmentTree as ending – starting + 1 segmentTree[node].
- Check if it is not a leaf node, then set or invert the value of boolTree of children.
- If the values are out of range, then return.
- Check if the segmentTree come in range, if true, then update the value current element of segmentTree as the difference and check again if it is not a leaf node, and do the same procedure as in step 2.
- Check if the segmentTree is not in range and values are lapping on either side of the segmentTree then do recursive call.
- Update the value of the current node of segmentTree node as their children result.
For count query
- Check if the current node is out of the range, then return 0.
- Then see if the current node of boolTrees is true, if true, then mark the current node of boolTrees to false and update the current node value of segmentTree as the difference.
- Check if it is not a leaf node and invert the values of the children.
- Check if the segmentTree lies in the given range, then return the segmentTree[node].
- If not the then recursively call the function so that it not overlaps.
Explanation
We have given an array of n such that all its values are initialized to 0. We are going to perform given two queries that are toggle query which is to invert all the 0s into the 1s and all the 1s into the 0s within the given range. The count query is to count all the zeroes present within the given range. We are going to use segmentTree which is initialized as 0. So we convert it into 1s within the range.
Whenever the toggle function is called, we will be looking for the Boolean array we created as boolTree which was initialized as false, we will check if the boolTree’ current node value is true or false, if it is false means any of the updates has not been done till now. So we need to do it, and if it is true, first of all, we mark it as false, so we can use it later, and update the value of segmentTree at the current node as the sum of the difference of ending and starting and the difference of 1 and current node’s value of segmentTree. We will be checking for if it is not a leaf node, because if it is, we will not make operations after that. If it is not, then we will update the children node’s values as the Boolean values.
Check if the current segment of segmentTree is within a given range or not. If not then make recursive calls for such that the nodes segment comes within the given range.
The same thing is to do with the count function but with slightly a different approach. We will be checking is the current node should not be out of range if it then simply returns the value 0.
Check if the current node should not be marked with the current node of segmentTree. If true then update the current node as false, and update the current node’s values of segmentTree as the sum of the difference of ending and starting and the difference of 1 and current node of segementTree we have done in toggling function, again checking is it is not a leaf, then move forward with the updation of the children nodes. So far at this point, we did all the prerequisite methods to return the answer, for that we are going to check if the current segment of nodes lies within the given range and return the current value of segementTree node. Else recursively calls the function to make it within the range.
Implementation
C++ code to Count and Toggle Queries on a Binary Array
#include<iostream>
using namespace std;
const int MAX = 100000;
int segmentTree[MAX] = {0};
bool boolTree[MAX] = {false};
void toggle(int node, int starting, int ending, int rangeStart, int rangeEnding)
{
if (boolTree[node])
{
boolTree[node] = false;
segmentTree[node] = ending - starting + 1 - segmentTree[node];
if (starting < ending)
{
boolTree[node<<1] = !boolTree[node<<1];
boolTree[1+(node<<1)] = !boolTree[1+(node<<1)];
}
}
if (starting>ending || rangeStart > ending || rangeEnding < starting)
return ;
if (rangeStart<=starting && ending<=rangeEnding)
{
segmentTree[node] = ending-starting+1 - segmentTree[node];
if (starting < ending)
{
boolTree[node<<1] = !boolTree[node<<1];
boolTree[1+(node<<1)] = !boolTree[1+(node<<1)];
}
return;
}
int mid = (starting+ending)/2;
toggle((node<<1), starting, mid, rangeStart, rangeEnding);
toggle((node<<1)+1, mid+1,ending, rangeStart, rangeEnding);
if (starting < ending)
segmentTree[node] = segmentTree[node<<1] + segmentTree[(node<<1)+1];
}
int count(int node, int starting, int ending, int qs, int qe)
{
if (starting>ending || qs > ending || qe < starting)
return 0;
if (boolTree[node])
{
boolTree[node] = false;
segmentTree[node] = ending-starting+1-segmentTree[node];
if (starting<ending)
{
boolTree[node<<1] = !boolTree[node<<1];
boolTree[(node<<1)+1] = !boolTree[(node<<1)+1];
}
}
if (qs<=starting && ending<=qe)
return segmentTree[node];
int mid = (starting+ending)/2;
return count((node<<1), starting, mid, qs, qe) +
count((node<<1)+1, mid+1, ending, qs, qe);
}
int main()
{
int n = 5;
toggle(1, 0, n-1, 0, 1);
toggle(1, 0, n-1, 2, 3);
cout << count(1, 0, n-1, 1, 2) << endl;
toggle(1, 0, n-1, 1, 4);
cout << count(1, 0, n-1, 0, 2) << endl;
return 0;
}
2 1
Java code to Count and Toggle Queries on a Binary Array
class toggleAndCount
{
static final int MAX = 100000;
static int segmentTree[] = new int[MAX];
static boolean boolTree[] = new boolean[MAX];
static void toggle(int node, int starting,int ending, int rangeStart, int rangeEnding)
{
if (boolTree[node])
{
boolTree[node] = false;
segmentTree[node] = ending - starting + 1 - segmentTree[node];
if (starting < ending)
{
boolTree[node << 1] = !boolTree[node << 1];
boolTree[1 + (node << 1)] = !boolTree[1 + (node << 1)];
}
}
if (starting > ending || rangeStart > ending || rangeEnding < starting)
{
return;
}
if (rangeStart <= starting && ending <= rangeEnding)
{
segmentTree[node] = ending - starting + 1 - segmentTree[node];
if (starting < ending)
{
boolTree[node << 1] = !boolTree[node << 1];
boolTree[1 + (node << 1)] = !boolTree[1 + (node << 1)];
}
return;
}
int mid = (starting + ending) / 2;
toggle((node << 1), starting, mid, rangeStart, rangeEnding);
toggle((node << 1) + 1, mid + 1, ending, rangeStart, rangeEnding);
if (starting < ending)
{
segmentTree[node] = segmentTree[node << 1] +segmentTree[(node << 1) + 1];
}
}
static int count(int node, int starting,int ending, int qs, int qe)
{
if (starting > ending || qs > ending || qe < starting)
{
return 0;
}
if (boolTree[node])
{
boolTree[node] = false;
segmentTree[node] = ending - starting + 1 - segmentTree[node];
if (starting < ending)
{
boolTree[node << 1] = !boolTree[node << 1];
boolTree[(node << 1) + 1] = !boolTree[(node << 1) + 1];
}
}
if (qs <= starting && ending <= qe)
{
return segmentTree[node];
}
int mid = (starting + ending) / 2;
return count((node << 1), starting, mid, qs, qe) + count((node << 1) + 1, mid + 1, ending, qs, qe);
}
public static void main(String args[])
{
int n = 5;
toggle(1, 0, n-1, 0, 1);
toggle(1, 0, n-1, 2, 3);
System.out.println( count(1, 0, n-1, 1, 2));
toggle(1, 0, n-1, 1, 4);
System.out.println(count(1, 0, n-1, 0, 2));
}
}
2 1
Complexity Analysis for Count and Toggle Queries on a Binary Array
Time Complexity
O( q * log n) where “q” is the number of queries and “n” is the size of the array.
Space Complexity
O(n) where “n” is the size of the array.