Table of Contents
Problem Statement
Suppose you have an integer array. This array should be treated as a circular array. The last value of an array will be connected to the first array, an ⇒ a1. The problem “Maximize sum of consecutive differences in a circular array” asks to find out the maximum sum of the difference between each consecutive element. So you have to find the difference between a consecutive element. You are allowed to rearrange the array numbers. Such that the sum of their differences should be maximum.
Maximum sum = | a1 – a2 | + | a3 – a4 | + | an-1 – an | + | an – a1|
Example
arr[]={9, 8, 4, 2}22
Explanation
We can arrange the given array as 9, 2, 8, 4 then it will give
| 9 – 2 | + | 2 – 8 | + | 8 – 4 | + | 4 – 9 | = 22
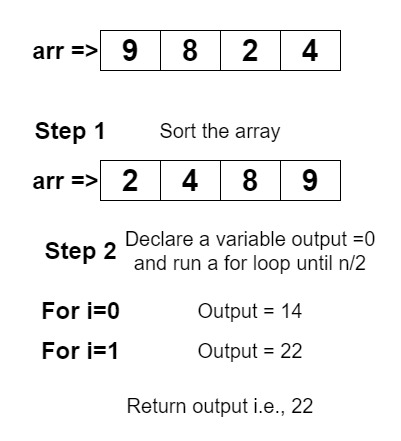
Algorithm
1. Set a variable output to 0.
2. Sort the given array.
3. Traverse up to n/2 length of the array(n is the length of the array).
1. Sum up the value of output and array’s last values and store it to sum.
2. Get the difference of output and twice of array’s starting value and store it to the output.
4. Return the value of output.Explanation
Given the array of integers. The array should be treated as a circular array which can be traversed to the first element directly after the last element. We have been asked to find out the maximum sum of the differences between the consecutive elements. And we have the advantage to rearrange the array. Such that we can maximize the sum of the differences.
Here we have given an array. We are not going to actually rearrange the array, we can simply play with its numbers. Now we are going to traverse only half of the array. That is only up to n / 2 length of the array where n is the actual length of the array. We have declared a variable called output. Which is going to get the differences of the array. And then sum up that and store it to output. But before traversing the array we are going to get the array sorted. We are going to sort the array such that it should be in increasing order. After sorting the array we have a number lowest in the array is at the starting of the array. And the greater number in the array is at the ending of the array.
Since we have sorted the array, we only need to traverse the array up to the half of the length of the array. Then we get the difference of twice of the current value of the array and the output value and store it to output. In this we get the difference, and then get the last value of the array, twice its value. And then add up with the output value and store it in output. Keep this process on till the half of the length of the array is reached and return the value of output.
Code
C++ code to Maximize sum of consecutive differences in a circular array
#include<iostream>
#include<algorithm>
using namespace std;
int getMaxDiff(int arr[], int n)
{
int output = 0;
sort(arr, arr + n);
for (int i = 0; i < n/2; i++)
{
output -= (2 * arr[i]);
output += (2 * arr[n - i - 1]);
}
return output;
}
int main()
{
int arr[] = { 9, 8, 2, 4 };
int n = sizeof(arr)/sizeof(arr[0]);
cout << getMaxDiff(arr, n) << endl;
return 0;
}
22
Java code to Maximize sum of consecutive differences in a circular array
import java.util.Arrays;
class maximumDiff
{
public static int getMaxDiff(int arr[], int n)
{
int output = 0;
Arrays.sort(arr);
for (int i = 0; i < n/2; i++)
{
output -= (2 * arr[i]);
output += (2 * arr[n - i - 1]);
}
return output;
}
public static void main (String[] args)
{
int arr[] = {9, 8, 2, 4 };
int n = arr.length;
System.out.println(getMaxDiff(arr, n));
}
}
22
Complexity Analysis
Time Complexity
O(n log n) where “n” is the number of elements in the array. Because we have sorted the array. So the time complexity becomes like that of merge sort. Since that marks the upper bound of the time complexity.
Space Complexity
O(1) as no extra space is required. So the space complexity required by the algorithm is constant. But the space complexity of the whole program is linear.