Table of Contents
Problem Statement
In this problem we have been given Row index(i) of the Pascal Triangle. We have to create a linear array containing the values of the ith row and return it. Row index starts from 0.
We know that Pascal’s triangle is a triangle where each number is the sum of the two numbers directly above it.
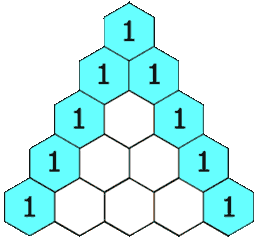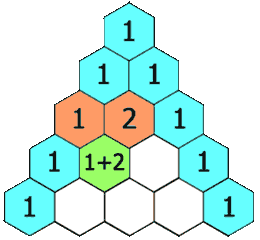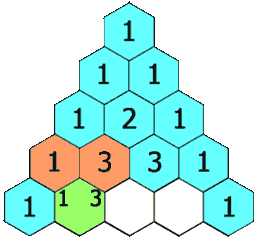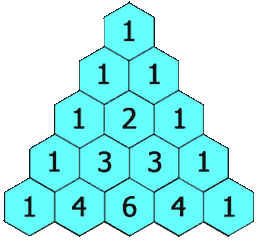
Example
rowIndex = 3
[1,3,3,1]
rowIndex = 0
[1]
As we know that each value in pascal’s triangle is a binomial coefficient (nCr) where n is the row and r is the column index of that value.
We have discussed similar problem where we have to return all the rows from row index 0 to given row index of pascal’s triangle here – Pascal Triangle Leetcode
But in this problem we only have to return single row whose index is given.
Here we will discuss three approaches for solution of this problem :
- Brute force
- Dynamic Programming
- Maths
Approach 1 (Brute Force Recursion)
We know that each number in this triangle is the sum of the two numbers directly above it. i.e
Num(row,col)= Num(row-1,col) + Num(row-1,col-1).
So we can repeatedly call the function Num(rowIndex,j) for each column index of that row, and return the formed list.
As we can see we have formulated recursive approach for finding Num(i,j). Now there are some base cases for that which are:
- Value at first row will be 1. So for row=0, Num(row, … ) =0.
- Value at first column will be 1. So for col=0, Num( … , col)=0.
- Last value of each row will be equal to 1. So for col=row=k, Num(k,k)=0.
Implementation for Pascal’s Triangle II Leetcode Solution
C++ Program
#include <bits/stdc++.h>
using namespace std;
int nCr(int n,int r)
{
if(n==0 || r==0 || r==n)
return 1;
return nCr(n-1,r-1)+ nCr(n-1,r);
}
vector<int> getRow(int rowIndex)
{
vector<int> res(rowIndex+1);
for(int i=0;i<=rowIndex;i++)
res[i]= nCr(rowIndex,i);
return res;
}
int main()
{
int rowIndex=3;
vector<int> ans= getRow(rowIndex);
for(auto val:ans) cout<<val<<" ";
cout<<endl;
return 0;
}1 3 3 1
Java Program
import java.util.*;
class Rextester{
static int nCr(int n,int r)
{
if(n==0 || r==0 || r==n)
return 1;
return nCr(n-1,r-1)+ nCr(n-1,r);
}
public static List<Integer> getRow(int rowIndex)
{
List<Integer> res=new ArrayList<Integer>();
for(int i=0;i<=rowIndex;i++)
res.add(nCr(rowIndex,i));
return res;
}
public static void main(String args[])
{
int rowIndex=3;
List<Integer> ans= getRow(rowIndex);
for(int val:ans) System.out.print(val+" ");
}
}
1 3 3 1
Complexity Analysis for Pascal’s Triangle II Leetcode Solution
Time Complexity
O(2^k): where k is the given Row Index.
We are calling recursion for Num(i,j) as Num(i-1,j)+Num(i-1,j-1). Hence time for finding Num(n,r) will be nCr.
We are calling this recursive function for all column index of given row (k).i.e
kC0+ kC1+ kC2+ …. +kCk = 2^k.
Hence total time complexity will be O(2^k).
Space Complexity
O(k): We need O(k) space to store all the values of given row in a list. Also at worst case our recursion will need O(k) stack space for recursive call. Hence O(k)+O(k) =~ O(k).
Approach 2 (Dynamic Programming)
In above recursion we can see that we are calling Num(i,j) function for same (i,j) repeatedly.
So what we can do is that we can memoize the ans for each (i,j) so that whenever there is need of calling that function again we return the cached answer directly from the memory without calculating again. Thus saving a lot of time.
For dynamically storing the answers we can use hash map where key will be the combination of row index and column index.
One more thing we can see here is that we need only previous row values for finding the values of the current row. Therefore we can store only one row values at a time and use it to find the values of next row. Hence we can reduce space complexity to O(k) here.
Space optimized Algorithm :
1. Create two arrays for previous row and current row respectively.
2. Initialise prev row as {1}.
3. Run a loop for ith row from i=1 to i=rowIndex. And generate new row values from previous row and store it in curr array.
4. Now update prev row by assigning cur row to prev row and repeat the same process in this loop.
5. Return the last row stored in prev array.
Implementation for Pascal’s Triangle II Leetcode Solution
C++ Program using Memoization
#include <bits/stdc++.h>
using namespace std;
unordered_map<string,int> cache;
int nCr(int n,int r)
{
string key= to_string(n)+to_string(r);
if(cache.count(key)) return cache[key];
if(n==0 || r==0 || r==n)
return 1;
return ( cache[key]= nCr(n-1,r-1)+ nCr(n-1,r) );
}
vector<int> getRow(int rowIndex)
{
vector<int> res(rowIndex+1);
for(int i=0;i<=rowIndex;i++)
res[i]= nCr(rowIndex,i);
return res;
}
int main()
{
int rowIndex=3;
vector<int> ans= getRow(rowIndex);
for(auto val:ans) cout<<val<<" ";
cout<<endl;
return 0;
}C++ Program ( Space optimized DP )
#include <bits/stdc++.h>
using namespace std;
vector<int> getRow(int rowIndex)
{
vector<int> prev={1},curr;
for(int i=1;i<=rowIndex;i++)
{
curr.clear();
curr.resize(i+1,1);
for(int j=1;j<i;j++)
curr[j]=prev[j]+prev[j-1];
prev=curr;
}
return prev;
}
int main()
{
int rowIndex=3;
vector<int> ans= getRow(rowIndex);
for(auto val:ans) cout<<val<<" ";
cout<<endl;
return 0;
}1 3 3 1
Java Program using Memoization
import java.util.*;
class Rextester{
static Map<String,Integer> cache=new HashMap<String,Integer>();
static int nCr(int n,int r)
{
String key= "" + n + r;
if(cache.containsKey(key)) return cache.get(key);
if(n==0 || r==0 || r==n)
return 1;
int ans= nCr(n-1,r-1)+ nCr(n-1,r);
cache.put(key,ans);
return ans;
}
public static List<Integer> getRow(int rowIndex)
{
List<Integer> res=new ArrayList<Integer>();
for(int i=0;i<=rowIndex;i++)
res.add(nCr(rowIndex,i));
return res;
}
public static void main(String args[])
{
int rowIndex=3;
List<Integer> ans= getRow(rowIndex);
for(int val:ans) System.out.print(val+" ");
}
}
Java Program ( Space optimized DP )
#include <bits/stdc++.h>
using namespace std;
vector<int> getRow(int rowIndex)
{
vector<int> prev={1},curr;
for(int i=1;i<=rowIndex;i++)
{
curr.clear();
curr.resize(i+1,1);
for(int j=1;j<i;j++)
curr[j]=prev[j]+prev[j-1];
prev=curr;
}
return prev;
}
int main()
{
int rowIndex=3;
vector<int> ans= getRow(rowIndex);
for(auto val:ans) cout<<val<<" ";
cout<<endl;
return 0;
}1 3 3 1
Complexity Analysis for Pascal’s Triangle II Leetcode Solution
Time Complexity
O(k^2): Memoization would make sure that a particular element is only calculated once. And assuming that it takes constant time to fetch ans from hash map it takes constant time to calculate each value of pascal’s triangle.
Now we end up calculating 1+2+3+…+(k+1)=(k+1)(k+2)/2 values which is =~ O(k^2).
Space Complexity
1. Simple memoization would hold all 1+2+3+…+(k+1)=(k+1)(k+2)/2 elements in the worst case. That would require O(k^2) space.
2. In space optimized DP we need O(k) space only to store the latest generated row.
Approach 3 (Maths)
As we know that each value in pascal’s triangle is a binomial coefficient (nCr). And we can write nCr as:
![]()
Now if we notice, successive binomial coefficients nC(r-1) and nCr differ by factor of :
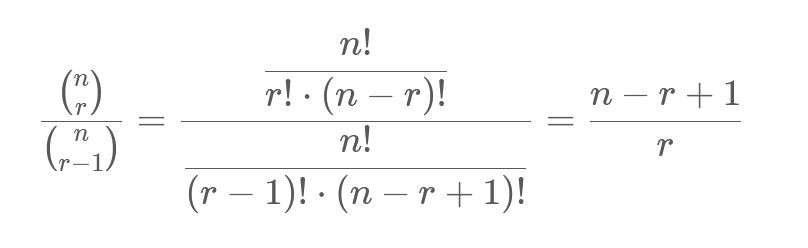
Thus, we can derive the next term in a row in Pascal’s triangle, from a preceding term.
Algorithm:
- Initialize first term of the row as 1.
- Run a loop for ith indexed column and calculate the next term (term(i)) as, term(i)= term(i-1)*(n-i+1)/i .
- Return the calculated values as a list.
Implementation for Pascal’s Triangle II Leetcode Solution
C++ Program
#include <bits/stdc++.h>
using namespace std;
vector<int> getRow(int rowIndex)
{
int n=rowIndex;
vector<int> res;
res.push_back(1);
for(int i=1;i<=n;i++)
{
int x= (int) ( ((long long)res.back()*(n-i+1) ) /i);
res.push_back(x);
}
return res;
}
int main()
{
int rowIndex=3;
vector<int> ans= getRow(rowIndex);
for(auto val:ans) cout<<val<<" ";
cout<<endl;
return 0;
}1 3 3 1
Java Program
import java.util.*;
class Rextester{
public static List<Integer> getRow(int rowIndex)
{
int n=rowIndex;
List<Integer> res=new ArrayList<Integer>();
res.add(1);
for(int i=1;i<=n;i++)
{
int x= (int) ( ((long)res.get(res.size()-1)*(n-i+1) ) /i);
res.add(x);
}
return res;
}
public static void main(String args[])
{
int rowIndex=3;
List<Integer> ans= getRow(rowIndex);
for(int val:ans) System.out.print(val+" ");
}
}
1 3 3 1
Complexity Analysis for Pascal’s Triangle II Leetcode Solution
Time Complexity
O(k): Each value of the row is calculated in constant time.
Space Complexity
O(k): No extra space is required other than for holding the output.