Table of Contents
Problem Statement
“Contiguous Array Leetcode” problem states that you are given an array a[ ] of size n consists of 1’s and 0’s only. Find the longest subarray in which the number of 1’s is equal to the number of 0’s.
Example
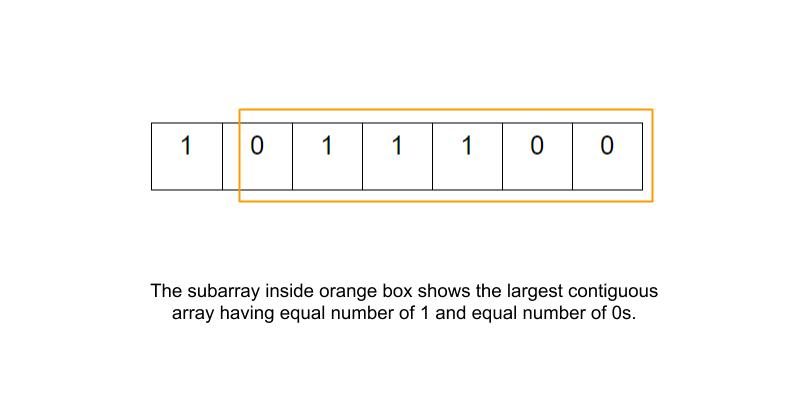
a[ ] = {1, 0, 1, 1, 1, 0, 0}1 to 6
Explanation: Choosing a subarray from index 1 to 6 gives us the best result of length 6. The contiguous array from 1 to 6 index has 3 zeros and 3 ones. Here we have considered 0 based indexing.
a[ ] = {1, 1}No such subarray
Approach
Naive Method
Generate all possible subarrays. Check if any exists any subarray in which the number of 1’s is equal to the number of 0’s. We use two pointers i and j for the left and right boundary of a subarray. Then we check if the sum of subarray from i to j has sum = 0, after replacing 0 with -1. If that’s true, we have found a subarray satisfying the conditions. Now we update our answer.
Algorithm for contiguous array leetcode problem
1. Initialize a binary array a[] of size n and three variables sum, max=-1, and start. 2. Traverse through the array and update sum as -1 if a[i] is 0 else 1. 3. Traverse the inner loop and add -1 in sum if a[i] is 0 else 1. 4. Check if the sum is 0 and max is less than j-i+1, update max as j-i+1 and start as i. 5. Outside the loops check if max is -1 print "No such subarray" else print starting and ending index.
Code
C++ Program to solve Contiguous Array Leetcode problem
#include <bits/stdc++.h>
using namespace std;
int subArray(int a[], int n){
int sum = 0;
int max = -1, start;
for(int i=0; i<n-1; i++){
sum = (a[i]==0) ? -1 : 1;
for(int j=i+1; j<n; j++){
(a[j]==0) ? (sum+=-1) : (sum+=1);
if(sum == 0 && max < j-i+1){
max = j-i+1;
start = i;
}
}
}
if(max == -1)
cout<<"No such subarray";
else
cout<<start<<" to "<<start+max-1;
return max;
}
int main(){
int a[] = { 1, 0, 1, 1, 1, 0, 0 };
int n = sizeof(a) / sizeof(a[0]);
subArray(a, n);
return 0;
}
1 to 6
Java Program to solve Contiguous Array Leetcode problem
class LongestSubArray{
int subArray(int a[], int n){
int sum = 0;
int max = -1, start=0,end=0;
for(int i=0; i<n-1; i++){
sum = (a[i]==0) ? -1 : 1;
for(int j=i+1; j<n; j++){
if(a[j] == 0)
sum += -1;
else
sum += 1;
if(sum == 0 && max < j-i+1){
max = j-i+1;
start = i;
}
}
}
if(max == -1)
System.out.println("No such subarray");
else
end = start+max-1;
System.out.println(start+" to "+end);
return max;
}
public static void main(String[] args){
LongestSubArray s = new LongestSubArray();
int a[] = { 1, 0, 1, 1, 1, 0, 0 };
int n = a.length;
s.subArray(a, n);
}
}
1 to 6
Complexity Analysis
Time Complexity
Since here we were traversing the array while keeping a pointer fixed. We attained a polynomial time complexity of O(N2) where n is the number of elements in the given array a[ ].
Space Complexity
O(1) because we used constant extra space. We only created a constant number of variables. But did not use any array other than the initial input array. But the program as a whole has O(N) space complexity because we used an array to store the input elements.
Using Hash map
Algorithm for contiguous array leetcode problem
1. Initialize a binary array a[] of size n. 2. Initialize an unordered map. 3. Traverse through the array and update the array value of the current index as -1 if current value if 0 else 1. 4. Traverse through the array and add the elements. 5. If the sum is 0, update max as i+1 and end as i. 6. Else Traverse map and update max as i - map(sum+n) and end as i if max is less than i - map(sum+n) else update map(sum+n) as i. 7. Traverse through the array and update the array value of the current index as 0 if current value is -1 else 1. 8. If the end is greater than -1 print starting and ending index. 9. Else print "No such subarray".
What we have done here, simply whenever we need to find the largest subarray having sum 0. What we do is we take the prefix sum and check-in our map if there is someplace where we can find the same sum. Then the subarray starting from the value stored in map +1 to the current index has sum 0. Here, we are using (sum + n) as the key. But we could have also used the sum directly. But if we use (sum+n ) as a key then we can also use an array instead of a HashMap. Because then we can assure that (sum+n) >=0 and array indexing start from 0.
Code
C++ Program to solve Contiguous Array Leetcode problem
#include <bits/stdc++.h>
using namespace std;
int subArray(int a[], int n){
unordered_map<int, int> hM;
int sum = 0, max = 0, end = -1;
for(int i=0; i<n; i++)
a[i] = (a[i] == 0) ? -1 : 1;
for(int i=0; i<n; i++){
sum += a[i];
if(sum == 0){
max = i + 1;
end = i;
}
if(hM.find(sum + n) != hM.end()){
if(max < i - hM[sum + n]){
max = i - hM[sum + n];
end = i;
}
}
else
hM[sum + n] = i;
}
for(int i=0; i<n; i++)
a[i] = (a[i] == -1) ? 0 : 1;
if(end>-1)
cout<<end - max + 1<<" to "<<end;
else
cout<<"No such subarray";
return max;
}
int main(){
int a[] = {1, 0, 1, 1, 1, 0, 0};
int n = sizeof(a) / sizeof(a[0]);
subArray(a, n);
return 0;
}
1 to 6
Java Program to solve Contiguous Array Leetcode problem
import java.util.HashMap;
class LongestSubArray{
int subArray(int a[], int n){
HashMap<Integer, Integer> hM = new HashMap<Integer, Integer>();
int sum = 0, max = 0, end = -1, start = 0;
for(int i=0; i<n; i++){
a[i]=(a[i]==0) ? -1 : 1;
}
for(int i=0; i<n; i++){
sum += a[i];
if(sum == 0){
max = i + 1;
end = i;
}
if(hM.containsKey(sum + n)){
if(max < i - hM.get(sum + n)){
max = i - hM.get(sum + n);
end = i;
}
}
else
hM.put(sum + n, i);
}
for(int i=0; i<n; i++) {
a[i] = (a[i] == -1) ? 0 : 1;
}
int index = end - max + 1;
if(end>-1)
System.out.println(index + " to " + end);
else
System.out.println("No such subarray");
return max;
}
public static void main(String[] args){
LongestSubArray s = new LongestSubArray();
int a[] = { 1, 0, 1, 1, 1, 0, 0 };
int n = a.length;
s.subArray(a, n);
}
}1 to 6
Complexity Analysis
Time Complexity
O(N) where n is the number of elements in the given array a[ ]. Since e used unordered_map/HashMap, we were able to achieve O(N) time because HashMap allows O(1) time to perform insertion searching, deletion.
Space Complexity
O(N) because we used N extra space. Since we used a HashMap ad stored the Information about N elements, in the worst case that can have N elements.