Heap sort is a comparison based sorting technique that is based on a Binary Heap data structure. HeapSort is similar to a selection sort where we find the maximum element and then place that element at the end. We repeat this same process for the remaining elements.
Table of Contents
Given an unsorted array, sort it using Heap Sort
Here the given input is an unsorted array and we have to sort the array using heap sort.
Input: 9,5,1,6,11,8,4
Output: 1,4,5,6,8,9,11
Heap Sort Algorithm
- HeapSort is a comparison-based algorithm, it places maximum element at the end of the array, repeats the process for remaining array elements until the whole of the array is sorted.
- Heap Sort builds a binary max-heap out of the array. Max heap is a tree data structure wherein every parent node is greater than its child node.
- Array arr[] can be represented as a binary Tree,
- arr[0] is root node.
- Index of left children = 2*i+1
- Index of right children = 2*i+2
Where i is the index of the parent node.
- Binary Tree is converted to binary heap using a Heapify operation, this operation maintains the value of the parent node which is greater than the child nodes (Max Heap). If the parent node is less than child nodes, then it swaps the parent with the child node with the greatest value.
Example of Max Heap Operation
Below is a max heap operation of a tree whose root value is 0, the left child is 5 and the right child is 4.
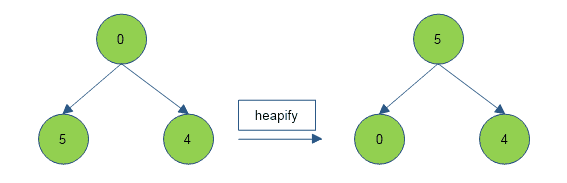
Algorithm
We use mainly two functions in a heap sort algorithm.
- heapServe(arr, i, n) – heapifies ith node of arr[]
- heapsort(arr, n) –
- it first heapifies the whole array (by heapifying non-leaf nodes).
- extracts the largest element at the root.
- replaces it with the last element of the array.
- repeats process a, b, c (in order) until we obtain a completely sorted array. Where a is heapServe(service function for heap sort), b is heapSort and c is extract root.

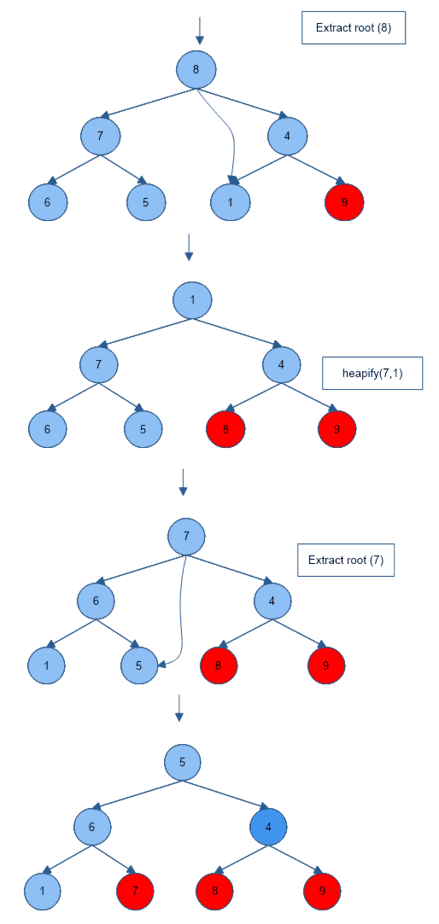
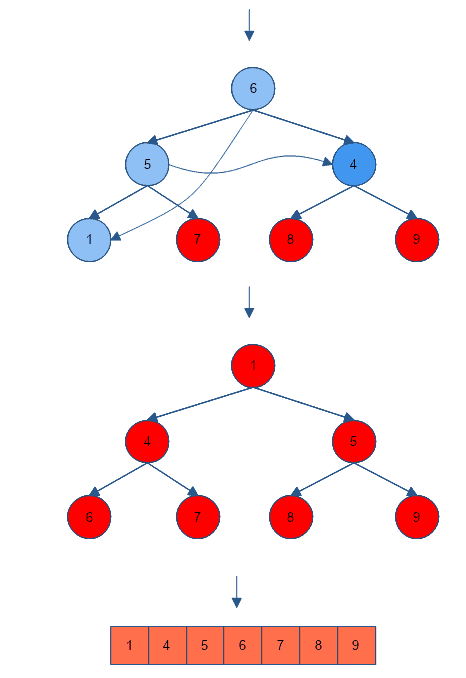
C++ Program for Heap Sort
#include <iostream>
using namespace std;
// service function to heapify array
void heapServe(int arr[],int i,int n)
{
int large = i;
// index of left and right child
int left = 2*i+1;
int right = 2*i+2;
// find largest amongst parent ,left and right children
if(left < n && arr[left] > arr[large])
large = left;
if(right < n && arr[right] > arr[large])
large = right;
// swap if parent node is not largest
// recursiveley heapify swapped nodes
if(large != i)
{
swap(arr[i],arr[large]);
heapServe(arr,large,n);
}
}
// function to sort the array
// Parent node is node that has atleast one children
void heapSort(int arr[],int n)
{
// Index of last/right most parent node
int last_non_leaf = n/2 - 1;
// heapify the array beginning from right most parent node
for(;last_non_leaf >= 0;last_non_leaf--)
heapServe(arr,last_non_leaf,n);
// start sorting from rightmost of the array
for(int i=n-1;i >= 0;i--)
{
// Extract root (largest) element,swap with last array element
swap(arr[0],arr[i]);
// heapify the leftover array (obtained after extracting largest element)
heapServe(arr,0,i);
}
}
int main()
{
int arr[] = {9,5,1,6,11,8,4};
int n = sizeof(arr)/sizeof(arr[0]);
heapSort(arr,n);
for(int i=0;i<n;i++)
cout<<arr[i]<<" ";
return 0;
}Output
1 4 5 6 7 8 9
Java Program for Heap Sort
class heap
{
// service function to heapify array
public static void heapServe(int arr[],int i,int n)
{
int large = i;
// index of left and right child
int left = 2*i+1;
int right = 2*i+2;
// find largest amongst parent ,left and right children
if(left < n && arr[left] > arr[large])
large = left;
if(right < n && arr[right] > arr[large])
large = right;
// swap if parent node is not largest
// recursiveley heapify swapped nodes
if(large != i)
{
int temp = arr[large];
arr[large] = arr[i];
arr[i] = temp;
heapServe(arr,large,n);
}
}
// function to sort the array
// Parent node is node that has atleast one children
public static void heapSort(int arr[],int n)
{
// Index of last/right most parent node
int last_non_leaf = n/2 - 1;
// heapify the array beginning from right most parent node
for(;last_non_leaf >= 0;last_non_leaf--)
heapServe(arr,last_non_leaf,n);
// start sorting from rightmost of the array
for(int i=n-1;i >= 0;i--)
{
// Extract root (largest) element,swap with last array element
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
// heapify the leftover array (obtained after extracting largest element)
heapServe(arr,0,i);
}
}
public static void main(String args[])
{
int arr[] = {9,5,1,6,11,8,4};
int n = arr.length;
heapSort(arr,n);
for(int i=0;i<n;i++)
System.out.print(arr[i]+" ");
}
}Output
1 4 5 6 7 8 9
Complexity Analysis of HeapSort
- Complexity of heapification is O(logn), extracting each element takes O(n) time, overall complexity T(n) = O(nlogn).
- Best case : T(n) = O(nlogn)
- Worst case : T(n) = O(nlogn)
- Average case : T(n) = O(nlogn)
- Auxiliary Space, A(n) = O(1)
Supplementary Information on HeapSort
- HeapSort is an Inplace Sorting Algorithm.
- Heap Sort is not a Stable Algorithm.
- Quicksort and Merge Sort often perform better than HeapSort as it has some constant time overhead due to recursive calls.
Reference
https://en.wikipedia.org/wiki/Heapsort