We are given an integer and the goal is to check whether the integer is a power of two, that is, it can be represented as some whole power of ‘2‘.
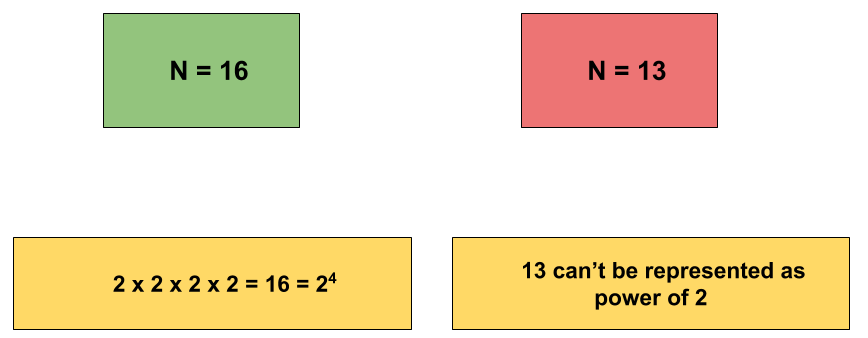
Table of Contents
Example
16
Yes
13
No
Approach
A trivial solution can be: Check if all prime factors of the integer are all ‘2‘. The time complexity of this method would be O(log2N). In order to do it in an optimal way, we can take help of Bit manipulations.
“Any number which is a power of two can only have a single bit set in binary representation”
How can it be checked that there is only a single bit set in the binary form?
Consider any number, x.
Now, if x is some power of two, then (x – 1) will turn off all the right bits to the set bit(set them as ‘0’) and the set bit would be unset.
x = 8[1000], x – 1 = 7[0111]
So, using BITWISE-AND of x and (x – 1), we can say if a number is some power of two, then, x & (x – 1) = 0
Algorithm(Trivial)
- Keep dividing the number by ‘2’ until it is not divisible by ‘2’ anymore.
- If the number is equal to ‘1’:
- The integer is a power of two
- Else
- The integer is not a power of two
Algorithm(Bit-Manipulation)
- Check if x & (x – 1) is equal to zero
- If yes, the number is a power of 2
- The integer is not a power of 2, otherwise
Implementation
C++ Program of Power of Two Leetcode Solution
Naive Method
#include <bits/stdc++.h>
using namespace std;
bool powerOfTwo(int n)
{
while(n % 2 == 0)
n /= 2;
return (n == 1);
}
int main()
{
int n = 16;
if(powerOfTwo(n))
cout << "Yes" << '\n';
else
cout << "No" << '\n';
return 0;
}
Optimal Method
#include <bits/stdc++.h>
using namespace std;
bool powerOfTwo(int n)
{
//16 = [10000]
//15 = [01111]
//16 & 15 = 0
return (n & (n - 1)) == 0;
}
int main()
{
int n = 16;
if(powerOfTwo(n))
cout << "Yes" << '\n';
else
cout << "No" << '\n';
return 0;
}
Yes
Java Program of Power of Two Leetcode Solution
Naive Method
class power_of_two
{
public static boolean powerOfTwo(int n)
{
while(n % 2 == 0)
n /= 2;
return (n == 1);
}
public static void main(String args[])
{
int n = 16;
if(powerOfTwo(n))
System.out.println("Yes");
else
System.out.println("No");
}
}
Optimal Method
class power_of_two
{
public static boolean powerOfTwo(int n)
{
return (n & (n - 1)) == 0;
}
public static void main(String args[])
{
int n = 16;
if(powerOfTwo(n))
System.out.println("Yes");
else
System.out.println("No");
}
}
Yes
Complexity Analysis
Time Complexity of Power of Two Leetcode Solution
The time complexity of Naive Approach is O(log2N), where N = given integer. However, the optimal approach is faster, as Bitwise-And is faster and therefore has a time complexity of O(1).
Space Complexity of Power of Two Leetcode Solution
Only space used in the program is the function signature. Therefore, constant space is used – O(1).