Find whether an array is subset of another array

Difficulty Level Easy
Frequently asked in Accolite GE Healthcare Qualcomm
Array Binary Search Hash Searching SortingViews 1835

The problem “Find whether an array is subset of another array” states that you are given two arrays arra1[] and array2[]. The arrays given are in an unsorted manner. Your task is to find whether the array2[] is a subset of array1[].

Example

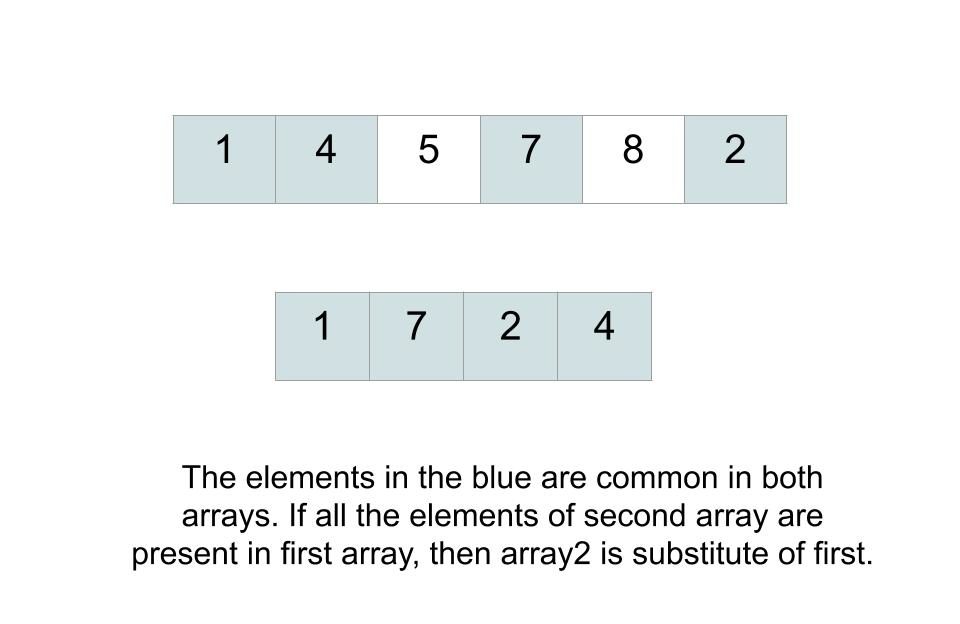
Find whether an array is subset of another array

arr1= [1,4,5,7,8,2]
arr2= [1,7,2,4]
arr2 [] is a subset of arr1 [].
arr1= [21,4,5,2,18,3]
arr2= [1,4,2,3]
arr2 [] is not a subset of arr1 [].

Algorithm

  1. Open a nested loop.
  2. Set i to 0, j to 0.
  3. While i is less than the length of array2[].
    1. While j is less than the length of array1[].
      1. If arr2[i] is equal to arr[j], then break.
  4. If j is equal to m, return false.
  5. Return true.

Explanation

Our task is to find whether the array second is a subset of array1. So our main idea is to use the nested loop and check each element and array2’s every element is found in array1, which means array2 is a subset of array1.

Let us take an example as our input in array1 and array2

Example

arr1[] = {11, 1, 13, 21, 3, 7}; arr2[] = {11, 3, 7, 1};

Starting with the 0th index of array2, we are going to check if the 0th index of arrays2 finds a similar number in array1[i], and yes it found it as 11. So we are going to break the loop and do i++.

Starting with the 1st index of array2[], we are going to check if the 1st index of arrays2 finds a similar number in array1[i], and yes it found it as 3. So we are going to break the loop and do i++.

Starting with the 2nd index of array2[], we are going to check if the 2nd index of arrays2 finds a similar number in array1[i] and it found it as 7. So we are going to break the loop and do i++.

Starting with the 1st index of array2[], we are going to check if the 1st index of arrays2 finds a similar number in array1[i] and 1 found it. So we are going to break the loop and do i++.

And about if condition which is represented as if ( j = = m ) this means, if in any of the iteration if any of array2’s element is not found in array1[], means it comes out of the loop without breaking it means ‘j’ with a value equal to the length of the array1[] that means we didn’t find one of the elements similar in array1[] and we return false because subset consists all of the element of the given set and we didn’t find one.

Code

C++ code to find whether an array is subset of another array

#include <iostream>
using namespace std;

bool isSubset(int arr1[], int arr2[], int l1, int l2)
{
    int i,j;
    for(i=0; i<l2; i++)
    {

        for(j=0; j<l1; j++)
        {
            if(arr2[i]==arr1[j])
                break;
        }
        if(j==l1)
            return false;
    }
    return true;
}
int main()
{
    int arr1[] = {1, 2, 3, 4, 5, 6};
    int arr2[] = {1, 3, 5};

    int l1=sizeof(arr1)/sizeof(arr1[0]);
    int l2=sizeof(arr2)/sizeof(arr2[0]);
    if(isSubset(arr1,arr2,l1,l2))
    {
        cout<<"arr2[] is a subset of arr1[]";
    }
    else
    {
        cout <<"arr2[] is not a subset of arr1[]"<<endl;
    }
    return 0;
}

arr2[] is a subset of arr1[]

Java code to find whether an array is subset of another array

class isArraySubset
{
    public static boolean isSubset(int arr1[],int arr2[], int l1, int l2)
    {
        int i = 0;
        int j = 0;
        for (i = 0; i < l2; i++)
        {
            for (j = 0; j < l1; j++)
            {
                if(arr2[i] == arr1[j])
                {
                    break;
                }
            }
            if (j == l1)
                return false;
        }
        return true;
    }
    public static void main(String args[])
    {
        int arr1[] = {1, 2, 3, 4, 5, 6};
        int arr2[] = {1, 3, 5};

        int l1 = arr1.length;
        int l2 = arr2.length;

        if(isSubset(arr1, arr2, l1, l2))
        {
            System.out.println("arr2[] is a subset of arr1[]");
        }
        else
        {
            System.out.println("arr2[] is not a subset of arr1[]");
        }
    }
}

arr2[] is a subset of arr1[]

Complexity Analysis

Time Complexity

O(m*n) where “m” is the size of arr1 and “n” is the size of arr2. Because we have used nested loops, making the time complexity polynomial.

Space Complexity

O(1), because we have not used any extra array/vector.

Translate »