The problem “Generate all possible sorted arrays from alternate elements of two given sorted arrays” states that suppose you have two sorted arrays. The problem statement asks to find out all the possible sorted arrays, such that number should be arranged alternatively from the two given different arrays.
Table of Contents
Example
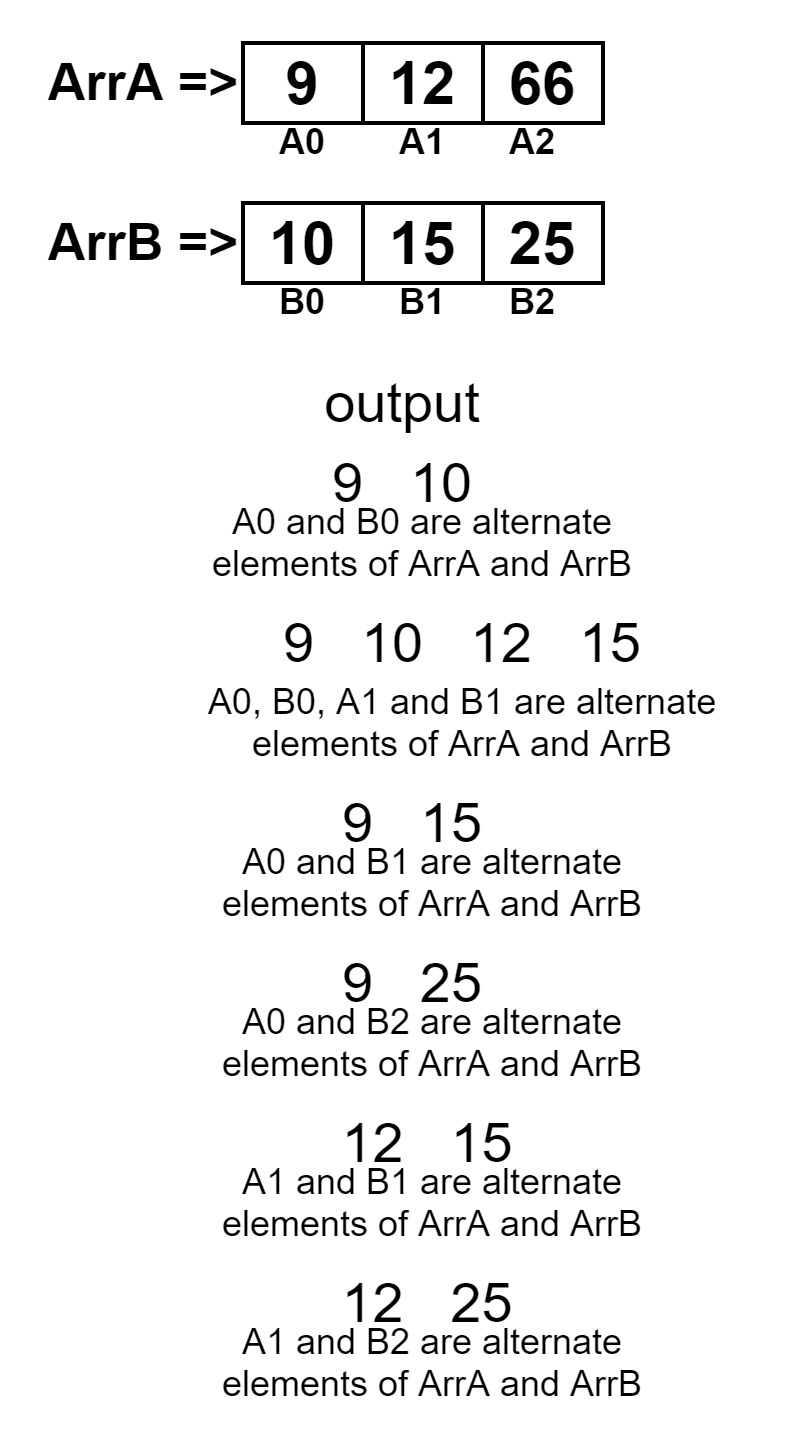
ArrA[] = {9, 12, 66}
ArrB[] = {10, 15, 25}9 10 9 10 12 15 9 10 12 25 9 15 9 25 12 15 12 25
Explanation
All the alternate numbers are from different arrays and sorted.
Algorithm
- Declare an output array of size m+n (total length of both the arrays).
- Check if boolCondition is true,
- Then check if the length of the output array is not equal to 0, then print the output array.
- Traverse the array ArrA and check the following
- If the length of the output array is 0 then copy the current element to the output array then recursively call the function.
- Traverse the array ArrA and check the following
- Else if the current array element is greater than the previous output array element, then copy the element from ArrA into the output array and recursively call the function.
- Then check if the length of the output array is not equal to 0, then print the output array.
- Else if boolCondition is false, then traverse the ArrB and check if the current element of ArrB is greater than the current element of the output array
- If true then copy the element from ArrB to the output array and recursively call the function.
Explanation
The problem “Generate all possible sorted arrays from alternate elements of two given sorted arrays” can be solved in the following manner. Here we are given two sorted arrays ArrA and ArrB. Both of the arrays given are in sorted order. So, we need to find out all the possible arrays which can be constructed in a sorted manner. There is also another condition that each alternate element in the output should come from different arrays.
We will recursively call that function to find out all the possible output arrays. Then we keep a boolean variable that keeps track of elements to be picked. That is either the element is from the current ArrA or ArrB. If the boolean variable is true, then we select an element from the first array ArrA. else if the boolean variable is false, then we select the element from the second array ArrB. If the Boolean variable is true, we are going to check if the length of the array is not equal to 0 or simply greater than 0, then every time we are going to print the output array.
We are going to traverse the array ArrA if the boolean condition is true. Then copy the current array element into the output array. Then we recursively call the function passing all the necessary arguments to it. If the boolean condition is false. Then we use ArrB to copy from and update our output array. And every time when the length of the output array is 0, then print the array.
Code
C++ code to generate all possible sorted arrays
#include<iostream>
using namespace std;
void printArray(int arr[], int n);
void getSortedArr(int ArrA[], int ArrB[], int output[], int i, int j, int m, int n, int len, bool flag)
{
if (flag)
{
if (len)
printArray(output, len+1);
for (int k = i; k < m; k++)
{
if (!len)
{
output[len] = ArrA [k];
getSortedArr(ArrA, ArrB, output, k+1, j, m, n, len, !flag);
}
else
{
if (ArrA [k] > output[len])
{
output[len+1] = ArrA [k];
getSortedArr(ArrA, ArrB, output, k+1, j, m, n, len+1, !flag);
}
}
}
}
else
{
for (int l = j; l < n; l++)
{
if (ArrB[l] > output[len])
{
output[len+1] = ArrB[l];
getSortedArr(ArrA, ArrB, output, i, l+1, m, n, len+1, !flag);
}
}
}
}
void generate(int ArrA [], int ArrB[], int m, int n)
{
int output[m+n];
getSortedArr(ArrA, ArrB, output, 0, 0, m, n, 0, true);
}
void printArray(int arr[], int n)
{
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
cout << endl;
}
int main()
{
int ArrA [] = {9, 12, 66};
int ArrB[] = {10, 15, 25};
int n = sizeof(ArrA)/sizeof(ArrA [0]);
int m = sizeof(ArrB)/sizeof(ArrB[0]);
generate(ArrA, ArrB, n, m);
return 0;
}
9 10 9 10 12 15 9 10 12 25 9 15 9 25 12 15 12 25
Java code to generate all possible sorted arrays
class GeneratedSortedArray
{
public static void getSortedArr(int ArrA[], int ArrB[], int output[], int i, int j, int m, int n, int len, boolean flag)
{
if (flag)
{
if (len!=0)
printArray(output, len+1);
for (int k = i; k < m; k++)
{
if (len==0)
{
output[len] = ArrA [k];
getSortedArr(ArrA, ArrB, output, k+1, j, m, n, len, !flag);
}
else
{
if (ArrA [k] > output[len])
{
output[len+1] = ArrA [k];
getSortedArr(ArrA, ArrB, output, k+1, j, m, n, len+1, !flag);
}
}
}
}
else
{
for (int l = j; l < n; l++)
{
if (ArrB[l] > output[len])
{
output[len+1] = ArrB[l];
getSortedArr(ArrA, ArrB, output, i, l+1, m, n, len+1, !flag);
}
}
}
}
public static void generate(int ArrA [], int ArrB[], int m, int n)
{
int output[]=new int[m+n];
getSortedArr(ArrA, ArrB, output, 0, 0, m, n, 0, true);
}
public static void printArray(int arr[], int n)
{
for (int i = 0; i < n; i++)
System.out.print(arr[i] + " ");
System.out.println();
}
public static void main(String [] args)
{
int ArrA [] = {9, 12, 66};
int ArrB[] = {10, 15, 25};
int n = ArrA.length;
int m = ArrB.length;
generate(ArrA, ArrB, n, m);
}
}
9 10 9 10 12 15 9 10 12 25 9 15 9 25 12 15 12 25
Complexity Analysis
Time Complexity
O(n1^2+n2^2) where “n1” and “n2” are the length of ArrA and ArrB. When the elements are alternating, that is ArrA[0] < ArrB[0] < ArrA[1] < ArrB[1]… In this case, we can have a total of n1^2 + n2^2 possible subsets. Thus a polynomial time complexity.
Space Complexity
O(n1+n2) where “n1” and “n2” are the length of ArrA and ArrB. Space is taken by the output array and since the size is n1 + n2. The space complexity is linear.