Table of Contents
Problem Statement
You are given two arrays of integers arr1[] and arr2[]. The problem “Sort an array according to the order defined by another array” asks to sort the first array according to the second array so that the numbers in first array will be relatively sorted off all the values in the arr2[]. And the elements in the first array which are not in the second array will be inserted at the end of the array in a sorted manner.
Example
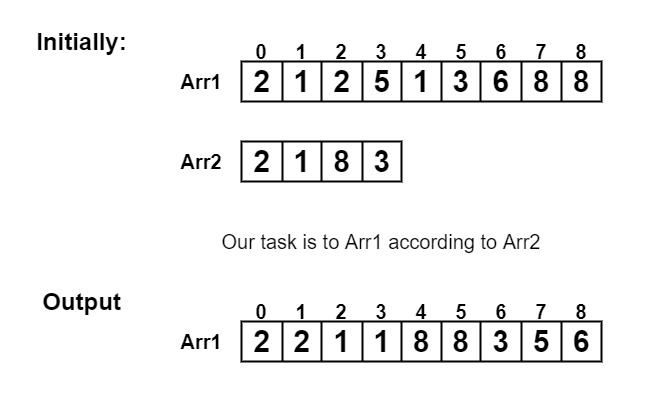
arr1[] = { 2,1,2,5,1,3,6,8,8 }
arr2[] = { 2,1,8,3}2 2 1 1 8 8 3 5 6
Explanation
A1 is sorted according to A2.
Algorithm to Sort an array according to the order defined by another array
1. Sort the array using the qsort method or comparator interface. 2. Search the value in arr2[] and find its index value. 3. Check if 1. Both of the returned value is -1 if true then return the difference between the returned value. 2. If one of the first returned values is -1 if true then return the -1. 3. If the second returned value is -1, then return 1. 4. Else return the value of the difference of the input value. 5. Print the sorted array.
Explanation
We have given the two integer arrays. Then we are asked to sort the first array according to the second array. One of the arrays is containing the whole values which are to be sorted. And the other array is containing few values in the order we have to sort the first array. That means if we have the number given in the second array as (1, 2, 3, 4). And we have to search for all 1s in the first array and put them first in a sorted manner in an array first. Then we have 2 in the second array. Find all of the 2s in the first array and then put them in the first array and so on.
We will be using the inbuilt method for finding out the desired result. In C++, we will be using the qsort method, qsort method is a predefined method used as a quicksort algorithm. It is one of the fastest algorithms to sort any list. And in java, we will be using the Comparator interface to sort the array according to the second array. The method will pick two of the values. For comparison, and then we will pass that value for searching out in the array second. If it is present in an array second is present then it will return the index for both of its values, it is not present, then we will return the value -1.
We have made some conditions. If we found both of the returned values as positive. Then we return the difference of returned values. If only the first value if positive then return -1. Else if only the second value is positive then return the 1. In case, none of the condition satisfies then return the difference of the picked values from the first array. After all of the comparisons, the array will be sorted. At last print the sorted array.
Code
C++ code to Sort an array according to the order defined by another array
#include <stdio.h>
#include<iostream>
using namespace std;
int Arr2[4];
int size = 4;
int searchElement(int key)
{
int i;
for (i = 0; i < size; i++)
if (Arr2[i] == key)
return i;
return -1;
}
int compareValuesFromArray(const void* a, const void* b)
{
int eleIndex1 = searchElement(*(int*)a);
int eleIndex2 = searchElement(*(int*)b);
if (eleIndex1 != -1 && eleIndex2 != -1)
return eleIndex1 - eleIndex2;
else if (eleIndex1 != -1)
return -1;
else if (eleIndex2 != -1)
return 1;
else
return (*(int*)a - *(int*)b);
}
void sortAccAnotherArray(int A1[], int size1)
{
qsort(A1, size1, sizeof(int), compareValuesFromArray);
}
int main()
{
int Arr1[] = {1,4,2,4,6,4,7,2,2,3 };
int Arr2[]= {1,2,3,4};
int n = sizeof(Arr1) / sizeof(Arr1[0]);
sortAccAnotherArray(Arr1, n);
for (int i = 0; i <n; i++)
printf("%d ", Arr1[i]);
return 0;
}
1 2 2 2 3 4 4 4 6 7
Java code to Sort an array according to the order defined by another array
import java.util.*;
import java.util.Arrays;
class SortAnArray
{
private static int Arr1[] = { 1,4,2,4,6,4,7,2,2,3};
private static int Arr2[]= {1,2,3,4};
private static int size = Arr2.length;
public static int searchElement(int key)
{
int i;
for (i = 0; i < size; i++)
if (Arr2[i] == key)
return i;
return -1;
}
public static void sortAccAnotherArray(int A1[], int size1)
{
Integer[]sortedArr = Arrays.stream(A1).boxed().toArray(Integer[]::new);
Arrays.sort(sortedArr, new Comparator<Integer>()
{
public int compare(Integer o1, Integer o2)
{
int a = o1.intValue();
int b = o2.intValue();
int eleIndex1 = searchElement(a);
int eleIndex2 = searchElement(b);
if (eleIndex1 != -1 && eleIndex2 != -1)
return eleIndex1 - eleIndex2;
else if (eleIndex1 != -1)
return -1;
else if (eleIndex2 != -1)
return 1;
else
return (a - b);
}
});
int[] finalArr = Arrays.stream(sortedArr).mapToInt(Integer::intValue).toArray();
System.out.println(Arrays.toString(finalArr));
}
public static void main(String [] args)
{
int n = Arr1.length;
sortAccAnotherArray(Arr1, n);
}
}
[1, 2, 2, 2, 3, 4, 4, 4, 6, 7]
Complexity Analysis
Time Complexity
O(mn Logm) where “m” is the length of arr1 & “n” is the length of arr2. Since we have used qsort ( sorting algorithm ). We have achieved the O(n log n) factor. Here the searching is done using linear search. And instead of doing that, we could have easily used a HashMap which would have reduced the time complexity even further.
Space Complexity
O(log n), where “m” and “n” is the length of Arr1 and Arr2. Because we have done sorting using quick sort so space complexity is because of that. But the program as a whole takes O(N+M).