Largest Subarray with Equal Number of 0’s and 1’s

Difficulty Level Medium
Frequently asked in Adobe Amazon Apple Facebook Google Quora Robinhood
Array Hash Hashing HashMapViews 3005

Problem Statement

In the “Largest Subarray with Equal Number of 0’s and 1’s” problem, we have given an array a[] containing only 0 and 1. Find the largest subarray with an equal number of 0’s and 1’s and will print the start index and end index of the largest subarray.

Input Format

The first line containing an integer value N.

Second-line containing N space-separated integers(0 or 1).

Output Format

The first and only one line containing an integer value denoting the length of the largest subarray with an equal_number of 0’s and 1’s.

Constraints

  • 1<=N<=10^5
  • 0<=a[i]<=1

Example

7
0 1 0 1 1 0 0
6

Approach

We use a variable sum to store the running sum when we encounter 1 we add 1 to the sum and when we encounter 0 we add -1 to the sum. We store all the sum in a map with their sum as key and index as value, as a key-value pair. If we encounter a sum that was discovered earlier that means between the last occurrence of that sum and this occurrence we have an equal number of 1 and -1. We take the max of all.

Let’s take a variable sum equals to 0 and traverse through the array. Every time we meet a 0, we decrease sum by 1 and increase sum by 1 when we meet 1. It’s pretty easy to conclude that we have a contiguous subarray with an equal number of 0 and 1 when count equals 0.

Lets take an array sequence [0, 0, 1, 0, 0, 0, 1, 1].

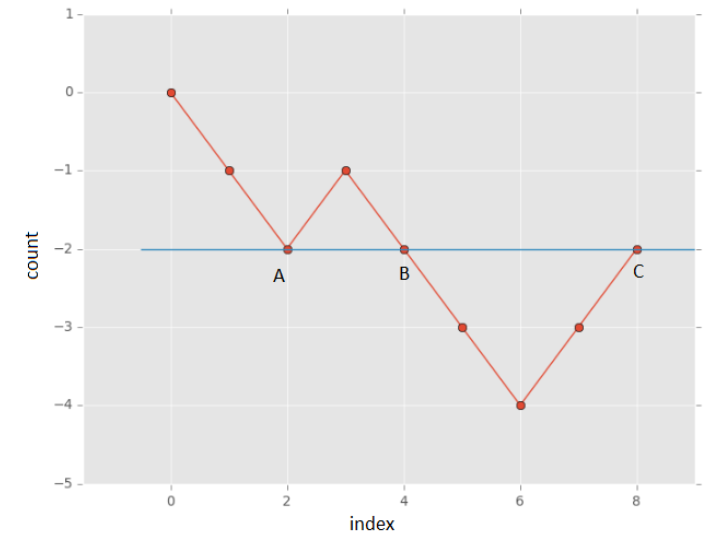
Largest Subarray with Equal Number of 0's and 1's

The sum starts from 0 and goes like this -1,-2, -1, -2, -3, -4, -3, -2

From the figure, we can easily understand that two points with the same y-axis value indicate the sequence between these two points has an equal number of 0 and 1.

The subarray with equal no of 0 and 1 started and ended when the sum equals -2, -1, and -3. The longest is when the sum equals -2.

Implementation

C++ Program for Largest Subarray with Equal Number of 0’s and 1’s

#include <bits/stdc++.h>
using namespace std;

int main() {
  int n;
  cin>>n;
  int a[n];
  for(int i=0;i<n;i++) cin>>a[i];
  map<int,int> m;
    int ans=0,sum=0;
    for(int i=0;i<n;i++){
        int x = a[i];
        sum+=(x==1)?1:-1;
        
        if(sum==0){
        	ans =max(ans,i+1);
        }
        if(m.count(sum)){
            ans = max(ans,i-m[sum]);
        }else{
            m[sum]=i;
        }
    }
    cout<<ans<<endl;
  return 0;
}

Java Program for Largest Subarray with Equal Number of 0’s and 1’s

import java.util.*;
import java.lang.*;
import java.io.*;

public class Main
{
  public static void main (String[] args) throws java.lang.Exception
  {
    Scanner sc = new Scanner(System.in);
    int n = sc.nextInt();
    int[] arr = new int[n];
    for(int i=0;i<n;i++){
            arr[i]=sc.nextInt();
        }
        int ans = max_length(arr,n);
        System.out.println(ans);
        
  }
  
  public static int max_length(int[] arr,int n){
    Map<Integer, Integer> m = new HashMap<>();
    	int mx = 0, cnt = 0;
    	for(int i = 0;i < arr.length;i++) {
    		cnt+=(arr[i] == 1)?1:-1;
    		if(cnt == 0)
    			mx = Math.max(mx, i+1);    		
    		if(m.containsKey(cnt)) {
    			mx = Math.max(mx, i - m.get(cnt));
    		} else 
    			m.put(cnt, i);
    	}
    	return mx;
  }
}
9
0 1 1 0 0 1 1 1 0
6

Complexity Analysis for Largest Subarray with Equal Number of 0’s and 1’s

Time Complexity

O(n) where n is the size of the given array. Here we traverse the whole array only one time and perform the operation for each element in constant time. That’s why it leads us to linear time complexity.

Space Complexity

O(n) where n is the size of the given array. We use map to store all the sum with their sum as key and index as value. And the maximum size of the map is n where all values of the array are 0.

Translate ยป