Level Order Traversal of Binary Tree

Level Order Traversal of a given binary tree is the same as the BFS of the binary tree. Do we already know about what actually BFS is? if not then don’t need to feel bad just read the whole article and visit our previous articles for better understanding. BFS is a level order traversal in which we visit the nodes of a binary tree from left to right at every level.

Here is the example of BFS:

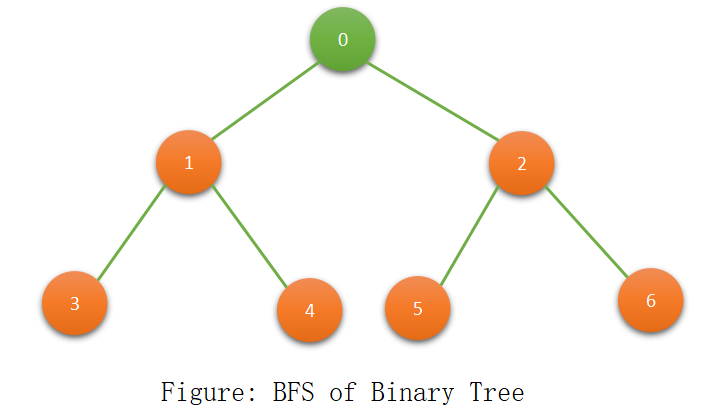
We are moving from left to right from every level and print the values:

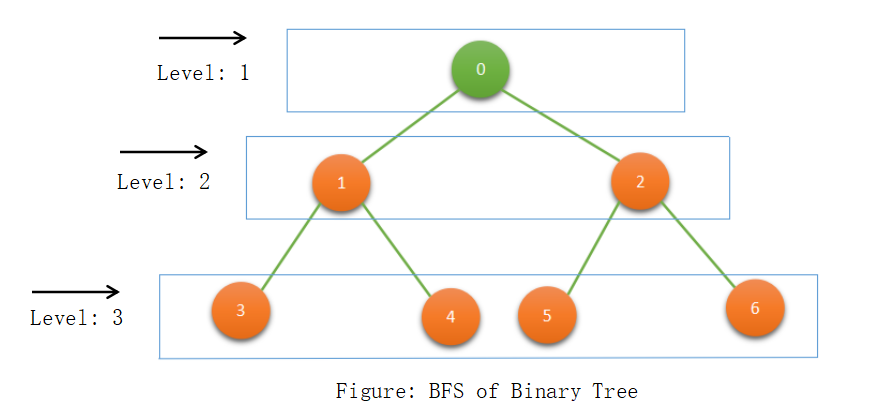
BFS of the above tree is 0,1,2,3,4,5,6.

By the use of the Queue data structure, we find the level order traversal. We start from root then we insert root into BFS and insert all neighbors of that node to queue. After that pop the node from the queue and add it to BFS if it is not visited and add it’s all neighbor (unvisited) to queue. Repeat it till the size of the queue is not equal to null.

Implementation For Level Order Traversal of Binary Tree

/*C++ Implementation to prin the BFS of given binary tree*/ 
#include<bits/stdc++.h> 
using namespace std; 
/*Structure of Node of BT which contain pointer to left child and right child and a data for node.*/ 
struct Node{ 
       int data; 
       struct Node* left;// for left child; 
       struct Node* right;// for right child; 
       Node(int value)// create a node using new Node; 
       { 
         data=value; 
         left=NULL; 
         right=NULL; 
       } 
}; 
/*Function which print level order of the given tree*/ 
void level_order(Node* root) 
{ 
    if(root==NULL) 
    { 
       return; 
    } 
    queue<Node*> q; 
    q.push(root); 
    while(!q.empty()) 
    { 
       Node* temp=q.front(); 
       cout<<temp->data<<" "; 
       q.pop(); 
       if(temp->left!=NULL) 
       { 
          q.push(temp->left); 
       } 
       if(temp->right!=NULL) 
       { 
           q.push(temp->right); 
       } 
    } 
    cout<<endl; 
} 
int main() 
{ 
     /*construct tree*/ 
     Node* root= new Node(0);//root node; 
     root->left= new Node(1); 
     root->right= new Node(2); 
     root->left->left= new Node(3); 
     root->left->right= new Node(4); 
     root->right->left= new Node(5); 
     root->right->right= new Node(6); 
     cout<<"Level order traversal of BT: "; 
     level_order(root); 
     return 0; 
}

Level order traversal of BT: 0 1 2 3 4 5 6

Time Complexity

O(N) where N is the number of nodes in the given binary tree.

Space Complexity

O(max_level) where max_level refers to the maximum number of elements in any level of a binary tree.

References