Combinations Leetcode Solution

Difficulty Level Medium
Frequently asked in Adobe Amazon Apple Facebook Google Microsoft Yahoo
algorithms Backtracking coding Interview interviewprep LeetCode LeetCodeSolutionsViews 5498

The problem Combinations Leetcode Solution provides us with two integers, n, and k. We are told to generate all the sequences that have k elements picked out of n elements from 1 to n. We return these sequences as an array. Let us go through a few examples to get a better understanding of the problem.

n = 4, k = 2
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

Explanation: The output shows all the ways of picking k elements out of first n natural numbers. Here, the ordering of the numbers does not matter. Only the collection of numbers matters.

n = 1, k = 1
[[1]]

Explanation: Here, since we have a single element. We are also told to pick a single element. Thus the output is [[1]].

Approach for the Combinations Leetcode Solution

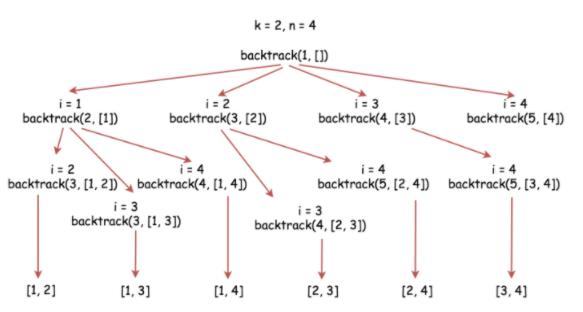
The problem Combinations Leetcode Solution asked us simply to generate all the sequences of picking k elements out of first n natural numbers. So, this is simply generating all the nCk combinations available to pick k elements. Generally, the tasks involving the generation of sequences are solved using recursion. So, we try a recursive approach to the problem. And keep track of a vector that aims to store such combinations.

So, we start with an empty vector. We push an element into it. Then recursively solve a subproblem of picking k-1 elements out of remaining n-1 elements. in this way we keep on reducing the problem until we reach the problem of picking 0 elements. When this happens, we push this temporary vector to our answer. In the end, this answer stores all the sequences of picking k elements out of n elements.

Combinations Leetcode Solution

Code for Combinations Leetcode Solution

C++ Code

#include <bits/stdc++.h>
using namespace std;

void rec(int i, int k, int n, vector<int>& cur, vector<vector<int>>& res){
    if(cur.size()==k) {
        res.push_back(cur);
    } else {
        for(int j=i;j<=n;j++) {
            cur.push_back(j);
            rec(j+1, k, n, cur, res);
            cur.pop_back();
        }
    }
}

vector<vector<int>> combine(int n, int k) {
    vector<vector<int>> res;
    vector<int> cur;
    rec(1, k, n, cur, res);
    return res;
}

int main(){
    vector<vector<int>> output = combine(4, 2);
    for(auto singleList: output){
        for(auto element: singleList)
            cout<<element<<" ";
        cout<<endl;
    }
}

1 2
1 3
1 4
2 3
2 4
3 4

Java Code

import java.util.*;
import java.lang.*;
import java.io.*;

class Main
{
  static List<List<Integer>> res = new ArrayList<List<Integer>>();
  
    public static void rec(int i, int k, int n, ArrayList<Integer> cur){
        if(cur.size()==k) {
            res.add(new ArrayList(cur));
        } else {
            for(int j=i;j<=n;j++) {
                cur.add(j);
                rec(j+1, k, n, cur);
                cur.remove(cur.size()-1);
            }
        }
    }
    
    public static List<List<Integer>> combine(int n, int k) {
        ArrayList<Integer> cur = new ArrayList<Integer>();
        rec(1, k, n, cur);
        return res;
    }

  public static void main (String[] args) throws java.lang.Exception{
    List<List<Integer>> res = combine(4, 2);
    System.out.println(res);
  }
}
[[1, 2], [1, 3], [1, 4], [2, 3], [2, 4], [3, 4]]

Complexity Analysis

Time Complexity

O(k*nCk), here nCk means the binomial coefficient of picking k elements out of n elements.

Space Complexity

O(nCk), as stated above the nCk here refers to the binomial coefficient.

Translate »