Find the Winner of the Circular Game LeetCode Solution

Problem Statement

Find the Winner of the Circular Game LeetCode Solution – There are n friends that are playing a game. The friends are sitting in a circle and are numbered from 1 to n in clockwise order. More formally, moving clockwise from the i^th friend brings you to the (i+1)^th friend for 1 <= i < n, and moving clockwise from the n^th friend brings you to the 1^st friend.

The rules of the game are as follows:

1. Start at the 1^st friend.
2. Count the next k friends in the clockwise direction including the friend you started at. The counting wraps around the circle and may count some friends more than once.
3. The last friend you counted leaves the circle and loses the game.
4. If there is still more than one friend in the circle, go back to step 2 starting from the friend immediately clockwise of the friend who just lost and repeating.
5. Else, the last friend in the circle wins the game.

Given the number of friends, n, and an integer k, return the winner of the game.

Example 1:

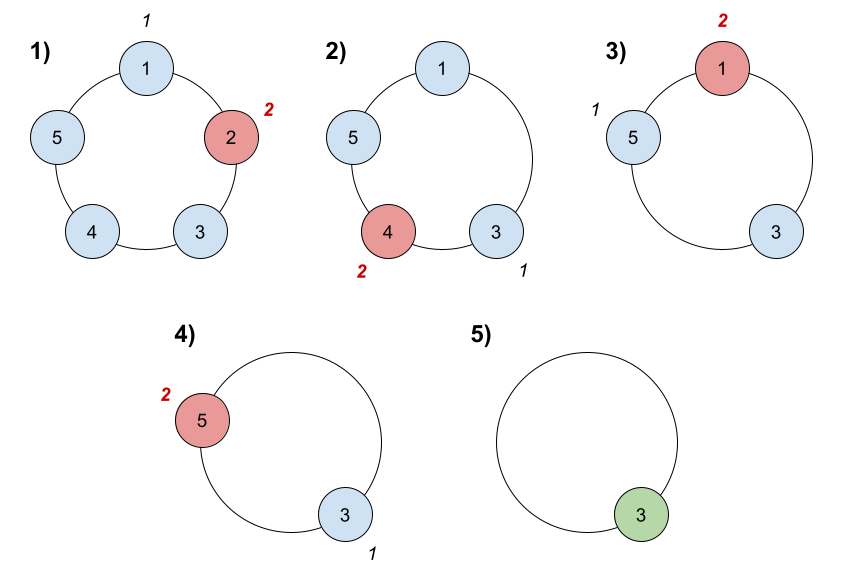Input:

 n = 5, k = 2

Output:

 3

Explanation:

 Here are the steps of the game:
1) Start at friend 1.
2) Count 2 friends clockwise, which are friends 1 and 2.
3) Friend 2 leaves the circle. Next start is friend 3.
4) Count 2 friends clockwise, which are friends 3 and 4.
5) Friend 4 leaves the circle. Next start is friend 5.
6) Count 2 friends clockwise, which are friends 5 and 1.
7) Friend 1 leaves the circle. Next start is friend 3.
8) Count 2 friends clockwise, which are friends 3 and 5.
9) Friend 5 leaves the circle. Only friend 3 is left, so they are the winner.

Approach

Idea:

If we know the winner index of (n – 1) persons, then we can find the winner index for n people. We can see this with an example with a group of 4 people with k being 2. We know that for 3 people (1,2,3) the winner is 3 (index 2) and this will come into play later. First, we eliminate one person out of 4 to make them 3, so for 1,2,3,4 -> we eliminate the kth person or person with (k – 1)th index, in this case being 2(index 1). Now we have 3 people remaining 1,3,4 with starting person as 3 (index 2) or person with (k + 1)th index for the next elimination, and we know that for 3 people, the winner will be the person at the 2nd index beginning with 3 as the starting point i.e. 1(index 0) or ((k + 1) + f(n – 1)) % n, where (k +1) is starting index and f(n – 1) is the answer for (n – 1) persons.

Code

Java Program of Find the Winner of the Circular Game:

class Solution {
   public int findTheWinner(int n, int k) {
        return findWinnerHelper(n, k - 1) + 1;
    }
    
    private int findWinnerHelper(int n, int k) {
        if (n == 1) {
            return 0;
        }
        
        return ((k + 1) % n + findWinnerHelper(n - 1, k)) % n;       
    }
}

C++ Program of Find the Winner of the Circular Game:

class Solution
{
    public:
    int findTheWinner(int n, int k)
    {
        return findWinnerHelper(n, k - 1) + 1;
    }
    private:
    int findWinnerHelper(int n, int k)
    {
        if (n == 1)
        {
            return 0;
        }
        return ((k + 1) % n + findWinnerHelper(n - 1, k)) % n;
    }
};

Python Program of Find the Winner of the Circular Game:

class Solution :
    def  findTheWinner(self, n,  k) :
        return self.findWinnerHelper(n, k - 1) + 1
    def  findWinnerHelper(self, n,  k) :
        if (n == 1) :
            return 0
        return ((k + 1) % n + self.findWinnerHelper(n - 1, k)) % n

Complexity Analysis for Find the Winner of the Circular Game LeetCode Solution

Time Complexity

The time complexity of the above code is O(1) because we don’t do any traverse anything, we just calculate the winner based on the number of players and k.

Space Complexity

The space complexity of the above code is O(1) because the amount of space used is always constant no matter how big n or k is since we aren’t actually traversing through the players.