Table of Contents
Problem Statement
In this problem there are houses in a street and House robber has to rob these houses. But the problem is that he can’t rob more than one house successively i.e which are adjacent to each other. Given a list of non-negative integers representing the amount of money of each house, we have to find out the maximum amount of money he can get.
Example
nums = [1,2,3,1]
4
Explanation: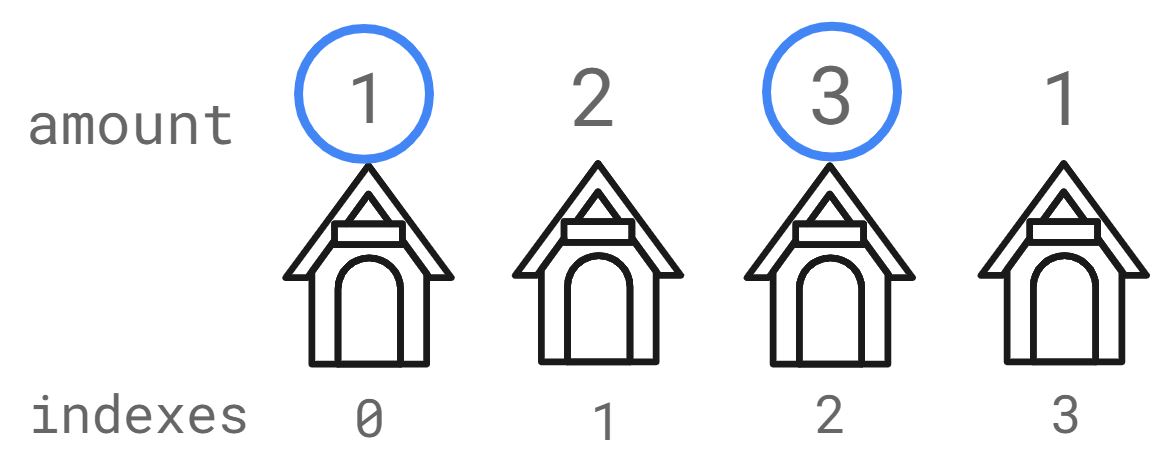
Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
nums = [2,7,9,3,1]
12
Explanation:
Rob house 1 (money = 2), rob house 3 (money = 9) and then 5th (money = 1).
Total amount you can rob = 2 + 9 + 1 = 12.
Approach
This problem can not be solved by greedy approach.
Let us take an example:
nums = [1,7,9,5,1,3,4]
If we would go for max element in the array(ie. 9), we would loose its adjacent sum (ie. 7+5). And best we can have is 15 as total sum.
If we go for even or odd position elements we have even sum=15 (7+5+3) and odd sum=15(1+9+1+4).
The optimum answer for this example will be [7+5+4]=12.
Hence to solve this type of problem we have to search for all choices recursively and pick out the maximum from them. Let us denote that:
f(n) = Largest amount that you can rob from first house to nth indexed house.
Ai = Amount of money at the ith index house.
At each house we have the choice of robbing it or leaving it.
case 1 – if we pick last house:
then, we cant pick (n-1)th house, hence f(n)= An + f(n-2)
case 2 – if we leave last house:
then, we will stick with the max profit till (n-1)th house, hence f(n)= f(n-1)
Let us see base cases.
n = 0, clearly f(0) = A0.
n = 1, then f(1) = max(A0, A1).
Hence we can summarize the formula as following :
f(n)= max( An + f(n-2) , f(n-1) )
This is a recursive formula which we can implement through simple recursion but here the time complexity will be O(2^n). Therefore we will use dynamic programming approach and store the intermediate results in an array.
After calculating we will return the value stored at nth(last) index in array.
Implementation
C++ Program for House Robber Leetcode Solution
#include <bits/stdc++.h>
using namespace std;
int rob(vector<int>& nums)
{
int n=nums.size();
if(n==0) return 0;
if(n==1) return nums[0];
int a[n];
a[0]=nums[0];
a[1]=max(nums[0],nums[1]);
for(int i=2;i<n;i++)
a[i]=max(nums[i]+a[i-2], a[i-1]);
return a[n-1];
}
int main()
{
vector<int> arr={1,2,3,1};
cout<<rob(arr)<<endl;
return 0;
}4
Java Program for House Robber Leetcode Solution
import java.util.*;
import java.lang.*;
class HouseRobber
{
public static int rob(int[] nums) {
int n=nums.length;
if(n==0) return 0;
if(n==1) return nums[0];
int a[]=new int[n];
a[0]=nums[0];
a[1]=Math.max(nums[0],nums[1]);
for(int i=2;i<n;i++)
a[i]=Math.max(nums[i]+a[i-2], a[i-1]);
return a[n-1];
}
public static void main(String args[])
{
int arr[]={1,2,3,1};
System.out.println(rob(arr));
}
}4
Complexity Analysis for House Robber Leetcode Solution
Time Complexity
O(n) : we are iterating from 1st house to nth house in a single loop, where n is the number of total houses.
Space Complexity
O(n) : we have used an array of size n to store the intermediate result.