Implement Trie (Prefix Tree) Leetcode Solution

Problem Statement

The Implement Trie (Prefix Tree) LeetCode Solution – “Implement Trie (Prefix Tree)” asks you to implement the Trie Data Structure that performs inserting, searching and prefix searching efficiently.

Example:

Input:  ["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]

Output: [null, null, true, false, true, null, true]

Explanation:

• After inserting all the strings, trie looks like this.

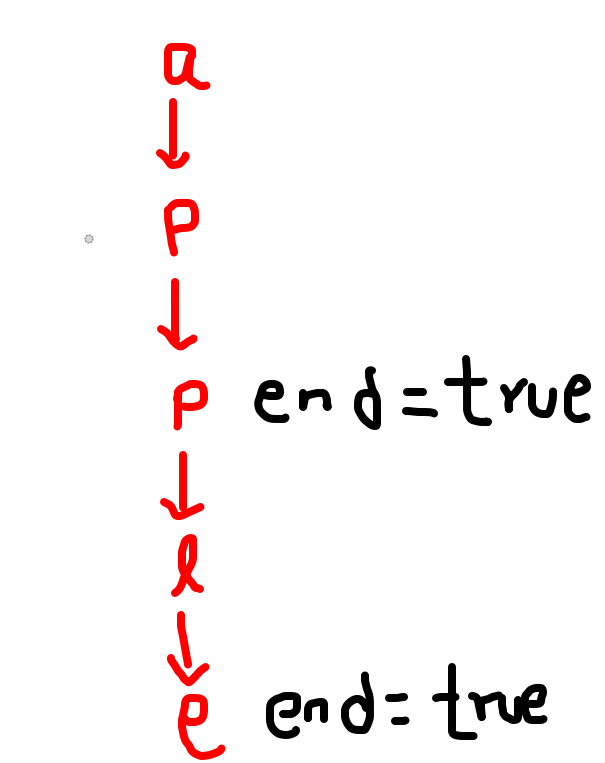
• Word apple is searched which exists, hence true.
• Word app is searched which is inserted later, hence first it outputs false, later true.

Approach

Idea:

1. The main idea to solve this problem is to create the Prefix Tree called a Trie data structure.
2. First, we’ll create a class TrieNode which will store two major pieces of information:
   1. Whether any word ends at this node or not?
   2. All the nodes are outgoing from the current node.
3. First, we’ll initialize the root node of the trie.
4. For every character in the input string, we’ll insert the node containing the current character in the trie if it doesn’t exist, otherwise, we’ll just move to that node. After inserting the string into a trie, we’ll mark the node where the string end as end = true.
5. For searching the string in the trie, we’ll search every character starting from the root node. At any step, when the next node doesn’t exist, return false. Also, at last, we need to check whether any word must end at this node, if yes return true.
6. For checking any prefix, start traversing from the root node for each character one by one. At any step, when a certain node doesn’t exist, return false. After checking for each character and every node that exists, return true finally.

Code

Implement Trie (Prefix Tree) Leetcode C++ Solution:

class Trie {
public:
    struct TrieNode{
        bool end;
        vector<TrieNode*> child;
        TrieNode(){
            end = false;
            child.assign(26,nullptr);
        }
    };
    TrieNode* root;
    Trie() {
        root = new TrieNode();
    }
    void insert(string word) {
        TrieNode* curr = root;
        for(auto& c:word){
            if(!curr->child[c-'a']){
                curr->child[c-'a'] = new TrieNode();
            }
            curr = curr->child[c-'a'];
        }
        curr->end = true;
    }
    bool search(string word) {
        TrieNode* curr = root;
        for(auto& c:word){
            if(!curr->child[c-'a']){
                return false;
            }
            curr = curr->child[c-'a'];
        }
        return curr->end;
    }
    bool startsWith(string prefix) {
        TrieNode* curr = root;
        for(auto& c:prefix){
            if(!curr->child[c-'a']){
                return false;
            }
            curr = curr->child[c-'a'];
        }
        return true;
    }
};

Implement Trie (Prefix Tree) Leetcode Java Solution:

class TrieNode {
    public char val;
    public boolean end;
    public TrieNode[] child = new TrieNode[26];
    public TrieNode() {}
    TrieNode(char c){
        TrieNode node = new TrieNode();
        node.val = c;
    }
}
public class Trie {
    private TrieNode root;
    public Trie() {
        root = new TrieNode();
        root.val = ' ';
    }
    public void insert(String word) {
        TrieNode curr = root;
        for(int i = 0; i < word.length(); i++){
            char c = word.charAt(i);
            if(curr.child[c - 'a'] == null){
                curr.child[c - 'a'] = new TrieNode(c);
            }
            curr = curr.child[c - 'a'];
        }
        curr.end = true;
    }
    public boolean search(String word) {
        TrieNode curr = root; 
        for(int i = 0; i < word.length(); i++){
            char c = word.charAt(i);
            if(curr.child[c - 'a'] == null) return false;
            curr = curr.child[c - 'a'];
        }
        return curr.end;
    }
    public boolean startsWith(String prefix) {
        TrieNode curr = root; 
        for(int i = 0; i < prefix.length(); i++){
            char c = prefix.charAt(i);
            if(curr.child[c - 'a'] == null) return false;
            curr = curr.child[c - 'a'];
        }
        return true;
    }
}

Complexity Analysis for Implement Trie (Prefix Tree) Leetcode Solution

Time Complexity

The time complexity of the above code is O(N*L) where N is the total number of calls made to search, insert, and starts with a function, and L is the maximum length of the parameter string.

The space complexity of the above code is O(N*L). It is the total space used to store nodes contained in the trie data structure.