Table of Contents
Problem Statement
The Longest Palindromic Substring LeetCode Solution – “Longest Palindromic Substring” states that You are Given a string s, return the longest palindromic substring in s.
Note: A palindrome is a word that reads the same backward as forwards, e.g. madam.
Example:
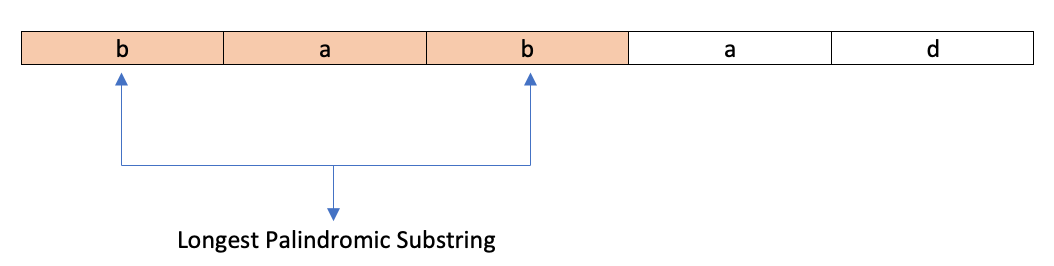
s = "babad"
"bab"
Explanation:
All the unique palindromic substrings are: “b”, “a”, “d”, “bab”, “aba”.
Out of these, “bab” and “aba” are the longest substrings.
s = "cbbd"
"bb"
Explanation:
All the unique palindromic substrings are: “c”, “b”, “d”, “bb”.
Out of these, “bb” is the longest substring.
Brute Force Solution
Idea:
We can check all the substrings and check which substrings are palindrome, then take the longest among them.
Code:
C++ Program of Longest Palindromic Substring LeetCode Solution
#include <bits/stdc++.h>
using namespace std;
bool check(string &s, int i, int j)
{
while (i <= j)
{
if (s[i] != s[j])
{
return false;
}
i++, j--;
}
return true;
}
string longestPalindrome(string s)
{
int n = s.length();
int max_len = 0;
int starting_index = 0;
for (int i = 0; i < n; i++)
{
for (int j = i; j < n; j++)
{
if (check(s, i, j))
{
if (j - i + 1 > max_len)
{
max_len = j - i + 1;
starting_index = i;
}
}
}
}
return s.substr(starting_index, max_len);
}
int main()
{
string s = "babad";
cout << longestPalindrome(s) << endl;
return 0;
}
bab
JAVA Program of Longest Palindromic Substring LeetCode Solution
public class TutorialCup {
public static Boolean check(String s, int i, int j) {
while (i <= j) {
if (s.charAt(i) != s.charAt(j)) {
return false;
}
i++;
j--;
}
return true;
}
public static String longestPalindrome1(String s) {
int n = s.length();
int max_len = 0;
int starting_index = 0;
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
if (check(s, i, j)) {
if (j - i + 1 > max_len) {
max_len = j - i + 1;
starting_index = i;
}
}
}
}
return s.substring(starting_index, starting_index + max_len);
}
public static void main(String[] args) {
String s = "babad";
System.out.println(longestPalindrome(s));
}
}
bab
Complexity Analysis
Time Complexity
The time complexity of the above code is O(n^3) because we are traversing over all the substrings and then checking each substring if it is a palindrome or not. There are n^2 substrings and checking a substring takes O(n) time, so total time complexity is O(n^3).
Space Complexity
The space complexity of the above code is O(1) because we are not using any extra space.
Optimized Solution
Idea:
The idea is again the same. For every substring, we will check if it is a palindrome or not, and if it is then we will take the longest among them. The only change is that now we will store if a substring is a palindrome or not in the “dp” array.
Now to check if a substring with starting index as “i” and ending index as “j” is a palindrome or not, we just have to check two conditions,
- If the ith and jth characters of the string are equal, and
- If substring with starting index as i+1 and ending index as j-1, is a palindrome.
If both the above conditions are true, then it means this substring is also a palindrome.
Code:
C++ Program of Longest Palindromic Substring
#include <bits/stdc++.h>
using namespace std;
int solve(vector<vector<int>> &dp, int i, int j, string &s)
{
if (dp[i][j] != -1)
{
return dp[i][j];
}
dp[i][j] = 0;
if (i == j)
{
return dp[i][j] = 1;
}
if (j - i == 1)
{
if (s[i] == s[j])
{
return dp[i][j] = 1;
}
else
{
return dp[i][j];
}
}
if (s[i] == s[j] && solve(dp, i + 1, j - 1, s) == 1)
{
return dp[i][j] = 1;
}
return dp[i][j];
}
string longestPalindrome(string s)
{
int n = s.length();
int max_len = 0;
int starting_index = 0;
vector<vector<int>> dp(n, vector<int>(n, -1));
for (int i = 0; i < n; i++)
{
for (int j = i; j < n; j++)
{
solve(dp, i, j, s);
if (dp[i][j] == 1)
{
if (j - i + 1 > max_len)
{
max_len = j - i + 1;
starting_index = i;
}
}
}
}
return s.substr(starting_index, max_len);
}
int main()
{
string s = "babad";
cout << longestPalindrome(s) << endl;
return 0;
}bab
JAVA Program of Longest Palindromic Substring
public class TutorialCup {
public static int solve(int[][] dp, int i, int j, String s) {
if (dp[i][j] != -1) {
return dp[i][j];
}
dp[i][j] = 0;
if (i == j) {
return dp[i][j] = 1;
}
if (j - i == 1) {
if (s.charAt(i) == s.charAt(j)) {
return dp[i][j] = 1;
} else {
return dp[i][j];
}
}
if (s.charAt(i) == s.charAt(j) && solve(dp, i + 1, j - 1, s) == 1) {
return dp[i][j] = 1;
}
return dp[i][j];
}
public static String longestPalindrome(String s) {
int n = s.length();
int max_len = 0;
int starting_index = 0;
int dp[][] = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dp[i][j] = -1;
}
}
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
solve(dp, i, j, s);
if (dp[i][j] == 1) {
if (j - i + 1 > max_len) {
max_len = j - i + 1;
starting_index = i;
}
}
}
}
return s.substring(starting_index, starting_index + max_len);
}
public static void main(String[] args) {
String s = "babad";
System.out.println(longestPalindrome(s));
}
}
bab
Complexity Analysis
Time Complexity
The time complexity of the above code is O(n^2) because we are traversing over all the substrings and then checking each substring if it is a palindrome or not. There are n^2 substrings and checking a substring takes O(1) time, so total time complexity is O(n^2).
Space Complexity
The space complexity of the above code is O(n^2) because we are using the dp array in which we are storing whether a substring is a palindrome or not.
Reference https://en.wikipedia.org/wiki/Palindrome