Table of Contents
Problem Statement
Possible Bipartition LeetCode Solution – We want to split a group of n people (labeled from 1 to n) into two groups of any size. Each person may dislike some other people, and they should not go into the same group.
Given the integer n and the array dislikes where dislikes[i] = [ai, bi] indicates that the person labeled ai does not like the person labeled bi, return true if it is possible to split everyone into two groups in this way.
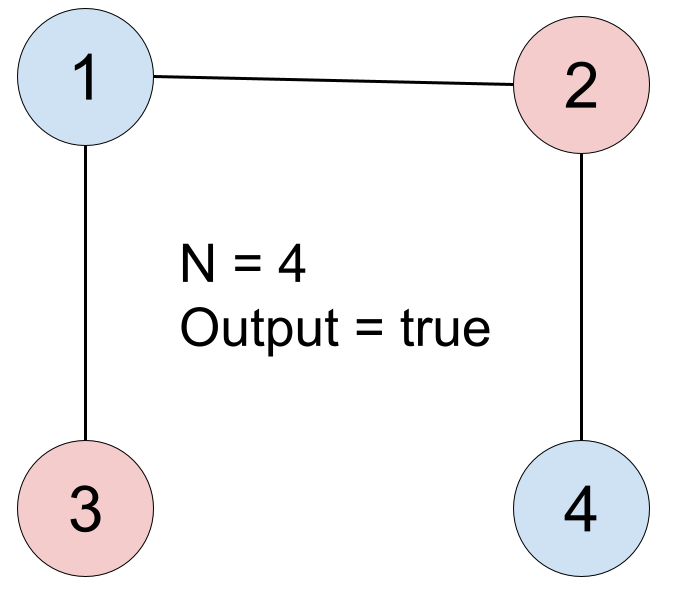
Input: n = 4, dislikes = [[1,2],[1,3],[2,4]] Output: true Explanation: group1 [1,4] and group2 [2,3].
Explanation
The question asks us to divide given people into two groups such that no two people in the same group dislike each other.
For ease of understanding, we can represent this problem as a graph, with people being the vertices and dislike-pairs being the edges of this graph.
We have to find out if the vertices can be divided into two sets such that there aren’t any edges between vertices of the same set. A graph satisfying this condition is called a bipartite graph.
We try to color the two sets of vertices, with RED and BLUE colors. In a bipartite graph, a RED vertex must be connected only with BLUE vertices and a BLUE vertex must be connected only with RED vertices. In other words, there must NOT be an edge connecting two vertices of the same color. Such an edge will be a conflict edge.
The presence of conflict edges indicates that bipartition is NOT possible.
The graph may consist of many connected components. For each connected component, we run our BFS algorithm to find conflict edges, if any. For each component, we start by coloring one vertex RED, and all its neighbors BLUE. Then we visit the BLUE vertices and color all their neighbors as RED, and so on. During this process, if we come across any RED-RED edge or BLUE-BLUE edge, we have found a conflict edge and we immediately return false, as bipartition will not be possible.
If no conflict edges are found at the end of the algorithm, it means bipartition is possible, hence we return true.
Code
C++ Code For Possible Bipartition
#define WHITE 0
#define RED 1
#define BLUE 2
class Solution {
public:
bool possibleBipartition(int N, vector<vector<int>> &edges)
{
vector<vector<int>> adj(N + 1);
vector<int> color(N + 1, WHITE);
vector<bool> explored(N + 1, false);
for (auto &edge: edges)
{
int u = edge[0];
int v = edge[1];
adj[u].push_back(v);
adj[v].push_back(u);
}
queue<int> q;
for (int i = 1; i <= N; ++i)
{
if (!explored[i])
{
color[i] = RED;
q.push(i);
// perform BFS from vertex i
while (!q.empty())
{
int u = q.front();
q.pop();
// check if u is already explored
if (explored[u])
{
continue;
}
explored[u] = true;
// for each neighbor of u, execute this loop
for (auto v: adj[u])
{
if (color[v] == color[u])
{
return false;
}
// we color v with the opposite color of u
if (color[u] == RED)
{
color[v] = BLUE;
}
else
{
color[v] = RED;
}
q.push(v);
}
}
}
}
return true;
}
};Python Code for Possible Bipartition
class Solution:
def possibleBipartition(self, N: int, dislikes: List[List[int]]) -> bool:
self.graph = collections.defaultdict(list)
group_mapping = {}
for (u, v) in dislikes: # Create graph
self.graph[u].append(v)
self.graph[v].append(u)
visited = set()
for i in range(1, N + 1): # Iterate each node
if i in visited: continue # No need to revisit, since it's a non-directed graph
stack = [(i, 0)] # Use stack for BFS
while stack: # You can also use a deque instead of 2 while loop on stack
tmp_stack = []
while stack: # exhaust current stack before go to next layer (BFS)
cur_node, group = stack.pop()
if cur_node in group_mapping and group != group_mapping[cur_node]: # check if it's conflict
return False
if cur_node in visited: continue # If visited and no conflict, continue to avoid dead loop
group_mapping[cur_node] = group # Assign group for current node
visited.add(cur_node)
for child in self.graph[cur_node]: # Assign contrary group for dislikes of current node
tmp_stack.append((child, not group))
stack = tmp_stack
return True
Java Code For Possible Bipartiton
class Solution {
public boolean possibleBipartition(int N, int[][] dislikes) {
int[] color = new int[N + 1];
List<List<Integer>> adj = new ArrayList<>(N + 1);
for(int i = 0; i <= N; i++) adj.add(new ArrayList<Integer>());
for(int[] d : dislikes) {
adj.get(d[0]).add(d[1]);
adj.get(d[1]).add(d[0]);
}
for(int i = 1; i <= N; i++) {
if(color[i] == 0) {
color[i] = 1;
Queue<Integer> q = new LinkedList<>();
q.add(i);
while(!q.isEmpty()) {
int cur = q.poll();
for(int nb : adj.get(cur)) {
if(color[nb] == 0) {
color[nb] = color[cur] == 1 ? 2 : 1;
q.add(nb);
} else {
if(color[nb] == color[cur]) return false;
}
}
}
}
}
return true;
}
}Complexity Analysis for Possible Bipartition LeetCode Solution
Time Complexity
O (N + E) since we take O(E) time to create an adjacency list and O (N) time to make a BFS traversal on it.
Space Complexity
O(N+E) since we store an adjacency list for the graph and also a visited array.