Unique Paths Leetcode Solution

The problem Unique Paths Leetcode Solution states that you are given two integers representing the size of a grid. Using the size of the grid, the length, and breadth of the grid. We need to find the number of unique paths from the top left corner of the grid to the bottom right corner. There is one another constraint on the direction of movement, at any point of time, one can move only in either down or right direction.

Example

row: 2, column: 2

2

Explanation: There are only two ways possible to complete the task. First either you move to the right or down. If you moved right you can move only down. If you had moved down, then you can move only in the down direction. So, only 2 ways are possible.

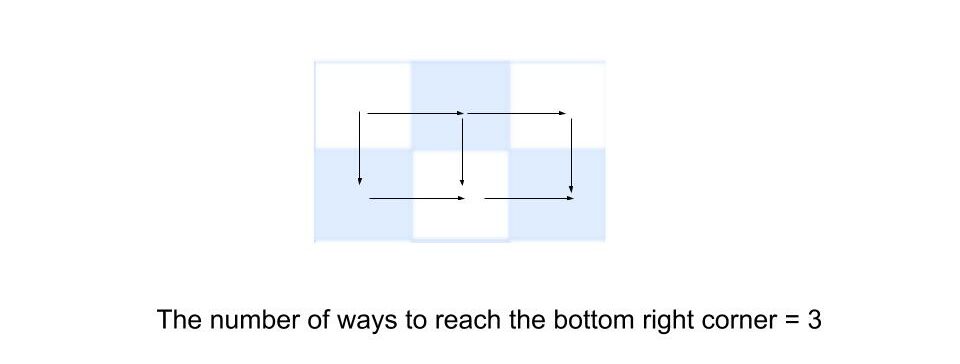
row: 2, column: 3

3

Explanation: There are 6 ways to reach destination. Consider if you moved to the right, then the problem has been reduced to the above example and you have 2 ways to reach the bottom right corner. If you would have down, then you have only a single way to reach the bottom right corner. Thus, the total number of ways to reach the end is 3.

Brute Force Approach for Unique Paths Leetcode Solution

The problem Unique Paths Leetcode Solution can be solved recursively. Just as we did in the second example, where we reduced the given problem into 2 subproblems. The same thing is what we will do in this solution. Once, we move to the right, then the problem is reduced to subproblem (row, column-1). If we had moved in the down direction, the problem is reduced into (row-1, column). We can easily code this recursive solution. But this will exceed the time limit because the solution is extremely inefficient.

Code for Brute Force Approach

C++ code

#include <bits/stdc++.h>
using namespace std;

int uniquePaths(int m, int n) {
    if(n==1 || m==1)return 1;
    return uniquePaths(m-1, n) + uniquePaths(m, n-1);
}

int main(){
    cout<<uniquePaths(2, 2);
}

2

Java Code

import java.util.*;
import java.lang.*;
import java.io.*;

class Solution {
    public static int uniquePaths(int m, int n) {
        if(m == 1 || n == 1)
            return 1;
        return uniquePaths(m-1, n) + uniquePaths(m, n-1);
    }
    
    public static void main(String[] args){
    	System.out.print(uniquePaths(2,2));
    }
}

2

Complexity Analysis

Time Complexity

O(2^max(m,n)), because of the exponential time complexity due to recursive function.

Space Complexity

O(max(m,n), the space used by the compiler stack. This depends on the height of the recursive tree.

Dynamic Programming Approach

The approach that has been explained above under the recursive solution can be easily memorized. Since the recursive function is dependent on two variables which are row, and column. Thus we create 2D DP array and store the result of each state. This will dramatically improve the time complexity because we are not resolving the same problems.

Dynamic Programming code for Unique Paths Leetcode Solution

C++ Code

#include <bits/stdc++.h>
using namespace std;

vector<vector<int>> dp;
int uniquePathsUtil(int m, int n) {
    if(m == 1 || n == 1) return 1;
    if(dp[m][n] != -1)
        return dp[m][n];
    return dp[m][n] = uniquePathsUtil(m-1, n) + uniquePathsUtil(m, n-1);
}

int uniquePaths(int m, int n) {
    dp.clear();
    dp.assign(m+1, vector<int>(n+1, -1));
    return uniquePathsUtil(m, n);
}

int main(){
    cout<<uniquePaths(2, 2);
}

2

Java Code

import java.util.*;
import java.lang.*;
import java.io.*;

class Solution {
    private static int uniquePathsUtil(int m, int n, int[][] dp) {
        if(m == 1 || n == 1) return 1;
        if(dp[m][n] != 0)
            return dp[m][n];
        return dp[m][n] = uniquePathsUtil(m-1, n, dp) + uniquePathsUtil(m, n-1, dp);
    }

    private static int uniquePaths(int m, int n) {
        int dp[][] = new int[m+1][n+1];
        return uniquePathsUtil(m, n, dp);
    }
    
    public static void main(String[] args){
    	System.out.print(uniquePaths(2,2));
    }
}

2

Complexity Analysis

Time Complexity

O(N*M), where N, M are used to represent the number of rows, and columns in the grid. Since there are a total of N*M states, the time complexity is also O(N*M).

Space Complexity

O(N*M), the space required is for creation of 2D DP table. The space complexity is polynomial for DP approach.