The problem “Pow(x, n) Leetcode Solution” states that you are given two numbers, one of which is a floating-point number and another an integer. The integer denotes the exponent and the base is the floating-point number. We are told to find the value after evaluating the exponent over the base. The base can be negative, positive, or zero. The exponent can lie anywhere between the range of an integer. We are also given a constraint on the output. The output will be anywhere between -10000 to +10000. So, let’s take a look at a few examples.
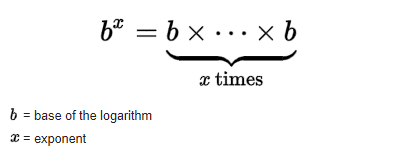
Table of Contents
Example
Base: 2 Exponent: 10
Answer: 1024
Explanation: Since the value for 2^10 = 104, hence the answer. This can also be checked by repetitive multiplication of 2 10 times.
Base: 2 Exponent: -10
Answer: 0.00098
Explanation: The answer has been changed because the value of the exponent has also been changed to -10.
Brute Force Approach
The brute force approach for the problem Pow(x, n) Leetcode Solution is very simple. We need to just simulate the operation of evaluating exponents. An exponent can easily be evaluated by multiplying the base exponent number of times. So, we can easily simulate this using a loop in any of our favorite programming languages. One thing to note, is the corner cases. When either the exponent is equal to the maximum value of integer or minimum value of integer. When we have exponent as the minimum value of integer, the answer can be either 1 or 0. If the base is 1 or -1, having exponent as integer’s minimum value, will have answer as 1 otherwise 0. Similarly we can have only 1 with exponent as maximum value of integer, because of the constraint on the output is below 10000. Considering these constraints we can write as brute force code with simulating the multiplication of base exponent times.
Code for Pow(x, n) Leetcode Solution
C++ Code
#include <bits/stdc++.h>
using namespace std;
double myPow(double x, int n) {
if (n == INT_MAX) return x;
else if (n == INT_MIN) return (x == 1 || x == -1) ? 1 : 0;
if(n<0) x=1/x, n*=-1;
double ans = 1;
for(int i=0;i<n;i++)
ans = ans*x;
return ans;
}
int main(){
cout<<myPow(2, 10);
}
1024
Java Code
import java.util.*;
import java.lang.*;
import java.io.*;
class Solution {
public static double myPow(double x, int n) {
if (n == Integer.MAX_VALUE) return x;
else if (n == Integer.MIN_VALUE) return (x == 1 || x == -1) ? 1 : 0;
if(n<0) {
x=1/x;
n*=-1;
}
double ans = 1;
for(int i=0;i<n;i++)
ans = ans*x;
return ans;
}
public static void main(String[] args){
System.out.println(myPow(2, 10));
}
};1024.0
Complexity Analysis
Time Complexity
O(N), because we loop until we multiply the base exponent times. Thus the time complexity is linear.
Space Complexity
O(1), because we have to store only the answer, we use a single variable. Thus, the space complexity is constant.
Optimized Approach for Pow(x, n) Leetcode Solution
The optimized approach uses the fast modulo exponentiation algorithm. We can implement fast modulo exponentiation either in a recursive manner or iteratively. In fast modulo exponentiation, we multiply the base in the power of 2. By this, we meant that we keep on multiplying the base by itself. So, in the first step, the base becomes squared of itself. Let’s suppose the base denoted by “b”. So in the first step, it becomes b^2, in the next step it will become b^4, then b^8, then b^16, and so on. Now, we multiply only the base powers corresponding to the ones in the exponent. So, convert exponent in binary format and keep on multiplying the bases as per the exponent binary format. For example, calculate 3^6. Here base =3, exponent = 6. Converting 6 in binary format makes it 110. Now, in the first step, we check if the exponent has 1. Since 6 has 0 as its first lowest significant bit, we skip it and the base becomes b^2. Now, 6 has 1 as its 2nd lowest significant bit, so we multiply b^2 to the answer. Now the answer is equal to b^2. The base then becomes b^4. Since 6 has 1 as its 3rd lowest significant bit, we multiply b^4 to the answer. The answer now becomes b^2 * b^4 = b^6. And this was what we wanted. Check the implementation below to find how to implement the algorithm.
Optimized code for Pow(x, n) Leetcode Solution
C++ code
#include <bits/stdc++.h>
using namespace std;
double myPow(double x, int n) {
if (n == INT_MAX) return x;
else if (n == INT_MIN) return (x == 1 || x == -1) ? 1 : 0;
if(n<0) x=1/x, n*=-1;
double ans = 1;
while(n>0){
if(n&1)
ans *= x;
x = x*x;
n = n>>1;
}
return ans;
}
int main(){
cout<<myPow(2, 10);
}
1024
Java code
import java.util.*;
import java.lang.*;
import java.io.*;
class Solution {
public static double myPow(double x, int n) {
if (n == Integer.MAX_VALUE) return x;
else if (n == Integer.MIN_VALUE) return (x == 1 || x == -1) ? 1 : 0;
if(n<0) {
x=1/x;
n*=-1;
}
double ans = 1;
while (n>0){
if(n%2 == 1) ans = ans*x;
x = x*x;
n = n>>1;
}
return ans;
}
public static void main(String[] args){
System.out.println(myPow(2, 10));
}
};1024
Complexity Analysis
Time Complexity
O(logN), because we used fast modulo exponentiation that takes logarithmic time to compute the exponent over a base. We can also intuitively find the time complexity. Since we have divided the exponent until it became 0. Thus the time required is dependent on logN, where N is the exponent.
Space Complexity
O(1), since we have used a single variable to store the answer, the space complexity is constant.